Assumendo che i risultati X, 1, 2 delle 13 partite di Totocalcio siano equiprobabili, calcolare la probabilità che tutte le partite, eccetto una, terminino in parità.
Soluzione 1
Probabilità degli eventi
- p(X) =

- p(1 oppure 2) =

- p(12 volte X su 13 partite) =
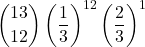 =
= 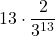 = 0,0000163… = 0,00163… %
= 0,0000163… = 0,00163… %
Soluzione 2
Eventi possibili
1111111111111 1111111111112 111111111111X ... 1XXXXXXXXXXXX
2111111111111 2111111111112 211111111111X ... 2XXXXXXXXXXXX
X111111111111 X111111111112 X11111111111X ... XXXXXXXXXXXXX
Eventi favorevoli
1XXXXXXXXXXXX 2XXXXXXXXXXXX X1XXXXXXXXXXX X2XXXXXXXXXXX XX1XXXXXXXXXX XX2XXXXXXXXXX
XXX1XXXXXXXXX XXX2XXXXXXXXX XXXX1XXXXXXXX XXXX2XXXXXXXX XXXXX1XXXXXXX XXXXX2XXXXXXX
XXXXXX1XXXXXX XXXXXX2XXXXXX XXXXXXX1XXXXX XXXXXXX2XXXXX XXXXXXXX1XXXX XXXXXXXX2XXXX
XXXXXXXXX1XXX XXXXXXXXX2XXX XXXXXXXXXX1XX XXXXXXXXXX2XX XXXXXXXXXXX1X XXXXXXXXXXX2X
XXXXXXXXXXXX1 XXXXXXXXXXXX2
Numero eventi possibili
![]()
Numero eventi favorevoli
13 · 2 = 26
Probabilità che tutte le partite, eccetto una, terminino in parità
![]()