Esame di Stato 2017 – 8

di

Un dado ha la forma di un dodecaedro regolare con le facce numerate da 1 a 12.
Il dado è truccato in modo che la faccia contrassegnata dal numero 3 si presenti con una probabilità p doppia rispetto a ciascun’altra faccia.
Determinare il valore di p in percentuale e calcolare la probabilità che in 5 lanci del dado la faccia numero 3 esca almeno 2 volte.

Quesito 1

Determinare il valore di p in percentuale

  • p_1+p_2+p_3+p_4+p_5+p_6+p_7+p_8+p_9+p_{10}+p_{11}+p_{12} = 1
  • p_1 = p_2 = p_4 = p_5 = p_6 = p_7 = p_8 = p_9 = p_{10} = p_{11} = p_{12}
  • p_3 = 2\cdot p_1
  • …
  • \displaystyle p_1 = p_2 = p_4 = p_5 = p_6 = p_7 = p_8 = p_9 = p_{10} = p_{11} = p_{12} = \frac{1}{13}
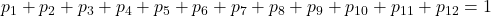
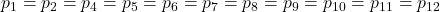
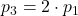
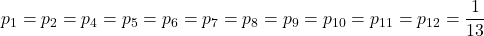
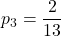  • \displaystyle p_3 = \frac{2}{13} = 0,153846… ~ 15,4 %

Quesito 2

Eventoprobabilità
Diverso da 3
in un lancio		\displaystyle 1-\frac{2}{13}= \displaystyle \frac{11}{13}= 0,84615~ 84,62 %
0 volte 3
in 5 lanci		\displaystyle {5 \choose 0}\left(\frac{2}{13}\right)^0\left(\frac{11}{13}\right)^5
= \displaystyle \frac{11^5}{13^5}		= \displaystyle \frac{161051}{371293}= 0,43375…~ 43,38 %
1 volta 3
in 5 lanci		\displaystyle {5 \choose 1}\left(\frac{2}{13}\right)^1\left(\frac{11}{13}\right)^4
= \displaystyle \frac{2\cdot 5\cdot 11^4}{13^5}		= \displaystyle \frac{292820}{371293}= 0,78764…~ 78, 77 %
Almeno 2 volte 3
in 5 lanci		\displaystyle 1-{5 \choose 0}\left(\frac{2}{13}\right)^0\left(\frac{11}{13}\right)^5-{5 \choose 1}\left(\frac{2}{13}\right)^1\left(\frac{11}{13}\right)^4
= \displaystyle 1-\frac{11^5}{13^5}-\frac{2\cdot 5\cdot 11^4}{13^5}
= …		= \displaystyle \frac{63832}{371293}= 0,1719…~ 17,2 %

Esercizio aggiuntivo

Calcola tutte le probabilità

EventoProbabilità
0 volte 3
in 5 lanci		\displaystyle {5 \choose 0}\left(\frac{2}{13}\right)^0\left(\frac{11}{13}\right)^5= \displaystyle 1\cdot \frac{11^5}{13^5}~ 0,433757
1 volta 3
in 5 lanci		\displaystyle {5 \choose 1}\left(\frac{2}{13}\right)^1\left(\frac{11}{13}\right)^4= \displaystyle 5\cdot \frac{2\cdot 11^4}{13^5}~ 0,394325
2 volte 3
in 5 lanci		\displaystyle {5 \choose 2}\left(\frac{2}{13}\right)^2\left(\frac{11}{13}\right)^3= \displaystyle 10\cdot \frac{2^2\cdot 11^3}{13^5}~ 0,143391
3 volte 3
in 5 lanci		\displaystyle {5 \choose 3}\left(\frac{2}{13}\right)^3\left(\frac{11}{13}\right)^2= \displaystyle 10\cdot \frac{2^3\cdot 11^2}{13^5}~ 0,026071
4 volte 3
in 5 lanci		\displaystyle {5 \choose 4}\left(\frac{2}{13}\right)^4\left(\frac{11}{13}\right)^1= \displaystyle 5\cdot \frac{2^4\cdot 11}{13^5}~ 0,002370
5 volte 3
in 5 lanci		\displaystyle {5 \choose 5}\left(\frac{2}{13}\right)^5\left(\frac{11}{13}\right)^0= \displaystyle 1\cdot \frac{2^5}{13^5}~ 0,000086