Integrazione numerica – Monte Carlo

di

Esercizio del libro di testo

Data la funzione \displaystyle 3x^2+2x+1 calcolare l’integrale definito della funzione da a=1 a b=5.

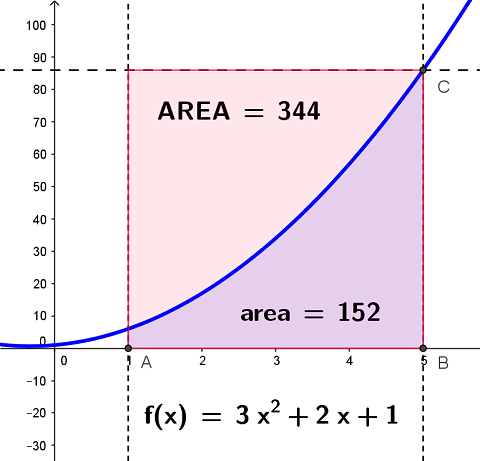
Nell’intervallo [1, 5] la funzione è continua, crescente.
Assume il valore massimo nell’estremo a destra, per x=5, MAX=f(5)=86.

Il grafico della funzione è compreso nel rettangolo individuato dai punti

  • A = (a, 0) = (1, 0)
  • B = (b, 0) = (5, 0)
  • C = (b, f(b)) = (5, 86)

Siano

  • x* ∈ [a, b], ascisse casuali
  • y* ∈ [0, MAX], ordinate casuali
  • PUNTI = numero di punti casuali generati
  • punti = numero di punti casuali con y* <= f(x*)
  • AREA = area del rettangolo
  • area = integrale definito

Osserva

  • AREA = (b-a)*f(b) = … = 344

Come approssimare il valore di area?

Per PUNTI abbastanza grande

\displaystyle \frac{\text{area}}{\text{AREA}} \approx \frac{\text{punti}}{\text{PUNTI}}

e quindi

\displaystyle \text{area}\approx \frac{\text{punti}}{\text{PUNTI}}\cdot \text{AREA}

Valore esatto

Il valore esatto, ricavato con il calcolo integrale, è

area = \displaystyle \int_a^b f(x)\ dx = \displaystyle \int_1^5 (3x^2+2x+1)\ dx = \dots = 152

Quindi

\displaystyle \frac{\text{area}}{\text{AREA}} = \displaystyle \frac{\text{152}}{\text{344}} = 0,44186…

Prova la simulazione realizzata con Javascript