Pi greco – Formule

Dato un cerchio qualsiasi pi greco è il rapporto tra le lunghezze della circonferenza e del diametro

$\displaystyle C = 2 \pi r$

$\displaystyle \pi = \frac{C}{2 r} = \frac{C}{d}$

Analogamente, pi greco è 4 volte il rapporto tra l’area del cerchio e l’area del quadrato circoscritto

$\displaystyle A = \pi r^2$

$\displaystyle \pi = \frac{A}{r^2} = ... = 4\cdot \frac{A}{d^2}$

Formule simili si possono ricavare da sfera, cilindro, cono, ellisse, …

La costante pi greco si ritrova in tutte le scienze applicate…

$e^{i \pi}+1=0$ , Eulero

$\displaystyle n!\approx \sqrt{2 \pi n} \left( \frac{n}{e} \right)^{n}$ , Formula di Stirling

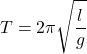$\displaystyle T=2\pi \sqrt{\frac{l}{g}}$ , Periodo di oscillazione del pendolo

$\displaystyle f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2 {\sigma}^2}}$ , Funzione di densità di probabilità: distribuzione normale

$\displaystyle\int_{0}^{+\infty}\,e^{-x^2}\,dx=\sqrt{\frac{\pi}{4}}$ , Gauss

$\displaystyle\int_{-\infty}^{+\infty}\,e^{-x^2}\,dx=\sqrt{\pi}$ , Gauss

$\displaystyle \int_{-\infty}^{+\infty}\,e^{-\frac{x^2}{2}}\,dx=\sqrt{2\pi}$ , Eulero

$\displaystyle\int_{-\infty}^{+\infty}\cos{(x^2)}\,dx=\sqrt{\frac{\pi}{2}$ , Fresnel

$\displaystyle\int_{-\infty}^{+\infty}\sin{(x^2)}\,dx=\sqrt{\frac{\pi}{2}$ , Fresnel

$\displaystyle\int_{-\infty}^{+\infty}\,\frac{1}{1+x^2}\,dx=\pi$

$\displaystyle\int_{0}^{1}\,\frac{1}{1+x^2}\,dx=\frac{\pi}{4}$

$\displaystyle\int_{-\infty}^{+\infty}\,\frac{\sin{x}}{x}\,dx=\pi$