1
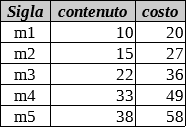
Nelle lezioni di educazione alimentare, i ragazzi hanno classificato alcuni alimenti in relazione al contenuto proteico e al loro costo
Trovare la lista L di costo minimo C della composizione alimentare che ha valore proteico totale pari a 48 unità.
2
Ho 5 anni più di mia sorella, che ne ha 7 meno di nostra cugina.
Quanti anni aveva nostra cugina quando la sua età era uguale alla somma delle nostre due?
3
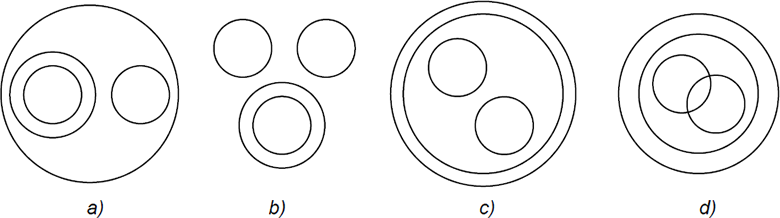
Quale tra i diagrammi sotto riportati rappresenta le relazioni esistenti fra i seguenti insiemi di numeri? INTERI – REALI – IMMAGINARI – COMPLESSI
4
Alcuni ragazzi decidono di realizzare un ipertesto multimediale sui monumenti della loro città.
Per valutare il tempo necessario a completare l’opera, dividono il lavoro complessivo in singole attività e ne stimano la durata in giorni.
Esiste un’attività iniziale, il cui avvio segna il tempo zero del progetto; le rimanenti attività potranno iniziare solo quando saranno state completate le rispettive attività propedeutiche, descritte da relazioni di priorità.
Le informazioni sullo schema organizzativo del progetto possono essere scritte in modo formale in due tabelle
Attività
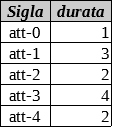
Priorità
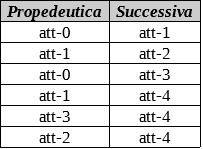
Indicare quanti giorni sono necessari per completare il progetto nel minor tempo possibile, tenendo presente che le attività tra loro non vincolate da relazioni di priorità possono essere svolte in parallelo.
5
Un salvadanaio contiene alcuni sacchetti di monete; su ogni sacchetto è riportato il valore complessivo delle monete che contiene.
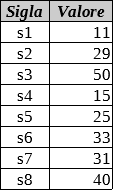
Il contenuto complessivo del salvadanaio è descritto da una tabella
Trovare la lista L1 dei sacchetti che spettano a Giorgio e la lista L2 di quelli che spettano ad Antonio sapendo che Antonio dovrà avere il sacchetto con il valore minore.
Nelle liste, i sacchetti vanno elencati in ordine crescente di sigla (s1 < s2 < … < s8).
 6
6
Un regista vuole sapere quante proiezioni del suo film sono state fatte in un certo cinema.
L’usciere del cinema in cui il film è stato proiettato gli fornisce queste informazioni:
- Alla prima proiezione c’era un solo spettatore
- A ogni nuova proiezione il numero degli spettatori è cresciuto di un’unità rispetto alla proiezione precedente
- Il numero totale di spettatori durante tutte le proiezioni è stato 820.
Quante proiezioni ci sono state?
 7
7
Federico ha trovato in soffitta tre scatole speciali.
La nonna gli ha detto che una di quelle tre scatole è piena di giocattoli mentre le altre due sono vuote, ma purtroppo potrà aprirne una sola.
Per fortuna il coperchio di ogni scatola riporta un’affermazione sul contenuto della scatola stessa:
- la scatola A riporta l’affermazione “I giocattoli non sono qui”
- la scatola B riporta l’affermazione “I giocattoli non sono qui”
- la scatola C riporta l’affermazione “I giocattoli sono nella scatola B”
La nonna svela un segreto a Federico: una e solo una delle tre affermazioni è vera!.
Dove sono i giocattoli?
- I giocattoli sono nella scatola A
- I giocattoli sono nella scatola B
- I giocattoli sono nella scatola C
- È impossibile che una e solo una delle tre affermazioni sia vera.
8
Date le seguenti assunzioni:
- Armando è un elettricista toscano
- Tutti gli elettricisti toscani leggono le opere del Boccaccio
- Chi legge le opere del Boccaccio non ha la televisione digitale terrestre
Quale delle seguenti affermazioni è vera?
- Armando preferisce leggere le opere del Boccaccio piuttosto che guardare la televisione
- Da quando c’è il digitale terrestre, ogni tanto Armando guarda la televisione, ma preferisce leggere le opere di Boccaccio
- Armando ignora l’esistenza della televisione digitale terrestre
- Non si può dire che Armando non conosca Boccaccio.
9
Se, nell’insieme dei numeri interi, vengono poste le seguenti condizioni:
- a = b+1
- b = c-2
- c = d+4
- e = d+2
Quale tra le seguenti affermazioni è vera?
- e > b
- e = b
- d > a
- a < c < b.
10
Un gioco è realizzato inserendo in una tavoletta tre pioli numerati con 1, 2, 3.
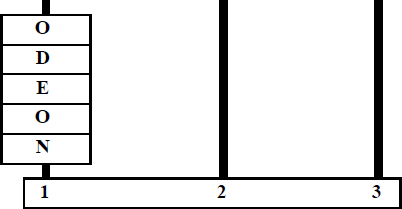
Sul piolo 3 c’è una pila di dischi, su ciascuno dei quali è incisa una lettera maiuscola in modo che dall’alto in basso si legga EDONO.
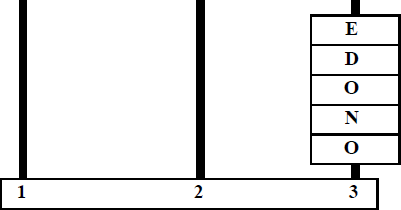
Si possono spostare i dischi prelevandoli uno alla volta dalla cima della pila di un piolo e infilandoli in un altro piolo: ciascun spostamento costituisce una mossa.
Qual è il numero minimo di mosse necessarie per trasferire i dischi al piolo 1 in modo che dall’alto in basso si legga ODEON?
11
Nego di non asserire che non affermo di non aver ragione, dunque:
- Dico che ho ragione
- Non dico che ho ragione
- Dico che non ho ragione
- Non dico che non ho ragione.
 12
12
Il grafo dei collegamenti bidirezionali fra 7 nodi (n1, n2, …, n7) è descritto da una tabella
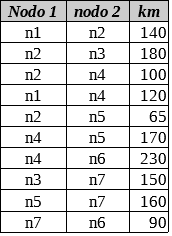
Trovare la lista L del percorso più breve dal nodo n1 al nodo n7 e calcolarne la distanza D in chilometri.