Algoritmo molto diffuso perché intuitivo ma con prestazioni scadenti.
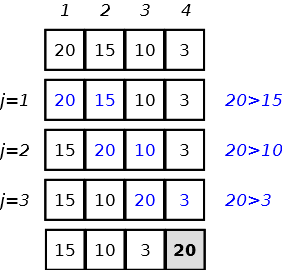Una passata
Una passata con ordinamenti di due elementi su tutte le n-1 coppie, all’interno di un array, provoca lo spostamento in alto della bolla più grande.
Sia
V=(20, 15, 10, 3)
alla fine della passata l’elemento più grande 20 si trova in ultima posizione
V=(15, 10, 3, 20)
|
1 2 3 |
For j:=1 To N-1 Do If(V[j] > V[j+1]) Then SCAMBIA(V[j], V[j+1]); |
Bubble sort
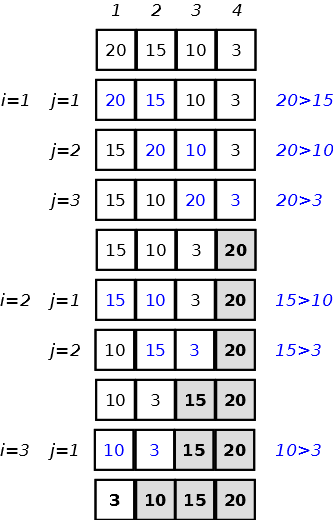
N passate, sulle n-1 coppie, ordinano sicuramente l’array
|
1 2 3 4 5 6 7 8 9 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var i, j: Integer; Begin For i:=1 To N Do For j:=1 To N-1 Do If(V[j] > V[j+1]) Then SCAMBIA(V[j], V[j+1]); End; |
In realtà sono necessarie al massimo N-1 passate su N-i coppie (di ciascuna passata)
|
1 2 3 4 5 6 7 8 9 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var i, j: Integer; Begin For i:=1 To N-1 Do For j:=1 To N-i Do If(V[j] > V[j+1]) Then SCAMBIA(V[j], V[j+1]); End; |
Osserva,,,
Miglioramenti?
Nel caso in cui il vettore risulti ordinato dopo un certo numero di passate è possibile interrompere l’esecuzione del While() introducendo la variabile ANCORA
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var ANCORA: Boolean; i, j : Integer; Begin i:=1; ANCORA:=True; While(i < N) And (ANCORA) Do Begin ANCORA:=False; For j:=1 To N-i Do If(V[j] > V[j+1]) Then Begin SCAMBIA(V[j], V[j+1]); ANCORA:=True; End; Inc(i); End; End; |
Il numero di passate dipende solo da ANCORA
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var ANCORA: Boolean; i, j : Integer; Begin i:=1; ANCORA:=True; While(ANCORA) Do Begin ANCORA:=False; For j:=1 To N-i Do If(V[j] > V[j+1]) Then Begin SCAMBIA(V[j], V[j+1]); ANCORA:=True; End; Inc(i); End; End; |
Se la variabile ANCORA non interviene si ha una passata in più.
Elimino la differenza N-i
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var ANCORA : Boolean; UltimaCoppia, j : Integer; Begin ANCORA:=True; UltimaCoppia:=N-1; While(Ancora) Do Begin ANCORA:=False; For j:=1 To UltimaCoppia Do If(V[j] > V[j+1]) Then Begin SCAMBIA(V[j], V[j+1]); ANCORA:=True; End; Dec(UltimaCoppia); End; End; |
La lunghezza del vettore dipende da UltimoScambio piuttosto che da UltimaCoppia
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var ANCORA : Boolean; UltimaCoppia , UltimoScambio, i : Integer; Begin ANCORA:=True; UltimaCoppia:=N-1; While(ANCORA) Do Begin ANCORA:=False; UltimoScambio:=1; For i:=1 To UltimaCoppia Do If(V[i] > V[i+1]) Then Begin SCAMBIA(V[i], V[i+1]); ANCORA:=True; UltimoScambio:=i; End; UltimaCoppia:=UltimoScambio-1; End; End; |
In questo modo le passate diventano più corte.
Il While…Do esterno diventa Repeat…Until
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var UltimaCoppia , UltimoScambio, i : Integer; FINITO : Boolean; Begin UltimaCoppia:=N-1; Repeat FINITO:=True; UltimoScambio:=1; For i:=1 To UltimaCoppia Do If(V[i] > V[i+1]) Then Begin SCAMBIA(V[i], V[i+1]); FINITO:=False; UltimoScambio:=i; End; UltimaCoppia:=UltimoScambio-1; Until(FINITO); End; |
Elimino la variabile FINITO
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Procedure BUBBLESORT(Var V: Vettore; N: Integer); Var UltimaCoppia , UltimoScambio, i : Integer; Begin UltimaCoppia:=N-1; Repeat UltimoScambio:=1; For i:=1 To UltimaCoppia Do If(V[i] > V[i+1]) Then Begin SCAMBIA(V[i], V[i+1]); UltimoScambio:=i; End; UltimaCoppia:=UltimoScambio-1; Until(UltimoScambio = 1); End; |
Complessità dell’algoritmo
L’istruzione SCAMBIA() viene eseguita ogni volta che ha successo il controllo dell’istruzione If(...) Then.
Consideriamo il caso pessimo, cioè che succeda a ogni passo.
Quanti sono i controlli e le esecuzioni di SCAMBIA()?
| i | j | Numero confronti | Numero scambi |
|---|---|---|---|
| 1 | 1…(n-1) | n-1 | n-1 |
| 2 | 1…(n-2) | n-2 | n-1 |
| … | … | … | … |
| n-2 | 1…(n-(n-2)) = 1…2 | 2 | 2 |
| n-1 | 1…(n-(n-1)) = 1…1 | 1 | 1 |
| Totale? | Totale? |
Quindi
TC(n)=TS(n)=(n-1)+(n-2)+...+1.
Quanto vale la somma?
Sappiamo che 1+2+...n=n(n+1)/2 e quindi
T(n)=(n-1)n/2=½n2-½n.
La complessità in tempo asintotica dell’algoritmo di ordinamento Bubble Sort è O(n2), sia per il numero di confronti che per il numero di scambi.
Nel caso ottimo, il vettore già ordinato, il numero di scambi è 0 ma rimane quadratico il numero di confronti.