Numeri di Fibonacci

di

Vedi la discussione

Esercizi

  1. Calcola la somma dei primi n numeri di Fibonacci.
    Visualizza i passi compiuti con una tabella e osserva: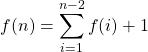 \displaystyle f(n)=\sum_{i=1}^{n-2} f(i) +1

    n f(n) Somma
    1 1 1
    2 1 2
    3 2 4
    4 3 7
    5 5 12
    6 8 20

    Quanto vale il rapporto tra due numeri di Fibonacci consecutivi?
    Prova per n crescente finché non raggiungi un’approssimazione adeguata e osserva: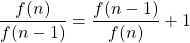  \dis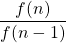playstyle \frac{f(n)}{f(n-1)} = \displaystyle \frac{f(n-1)}{f(n)}+1

    n f(n) \displaystyle \frac{f(n)}{f(n-1)} \displaystyle \frac{f(n-1)}{f(n)}
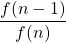
    1 1
    1 1 1 1
    2 1 2 0,5
    3 2 1,5 0,6…
    4 3 1,6… 0,625
    5 5 1,625 0,6153…
    … … … …
    … … 1,6180339… 0,6180339…

Complessità degli algoritmi

Dopo aver analizzato il problema e individuati i 3 algoritmi discutiamo la loro complessità in tempo.

Algoritmo ricorsivo: il tempo di attesa può essere considerato proporzionale al numero di chiamate ricorsive

  • T(1) = 1
  • T(2) = 1
  • T(3) = 1+T(2)+T(1) = 1+1+1 = 3 > 22-1
  • T(4) = 1+T(3)+T(2) = 1+3+1 = 5 > 22-1
  • T(5) = 1+T(4)+T(3) = 1+5+3 = 9 > 23-1
  • T(6) = 1+T(5)+T(4) = 1+9+5 = 15 > 23-1
  • T(7) = 1+T(6)+T(5) = 1+15+9 = 25 > 24-1
  • T(8) = 1+T(7)+T(6) = 1+25+15 = 41 > 24-1
  • …
  • T(n) \ge 2^{n/2}-1

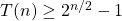
Il tempo di attesa è esponenziale, anche se con esponente n/2 piuttosto che n, quindi per n molto grande T(n) ∈ O(2n).

L’algoritmo ricorsivo per il calcolo dell’n-simo numero di Fibonacci ha complessità esponenziale!

Algoritmo iterativo: si tratta di un algoritmo con un’iterazione semplice, senza chiamate ricorsive, quindi

  • T(n) = c1+c2n
  • T(n) ∈ O(n).

L’algoritmo iterativo per il calcolo dell’n-simo numero di Fibonacci ha complessità lineare!

Con formula: se consideriamo costante il tempo necessario per svolgere le singole operazioni presenti nella formula allora

  • T(n) = c
  • T(n) ∈ O(1).

Se consideriamo che per n molto grande l’operazione di elevamento a potenza potrebbe dipendere dal numero di cifre e che il numero di cifre del risultato cresce proporzionalmente al logaritmo di n allora si ottiene T(n) ∈ O(log n).

Conclusioni

Metodo Pro Contro
Ricorsivo Formulazione molto semplice Numero esponenziale di passi!
Iterativo Ripetizione di operazioni elementari Molti passi se n è grande
Con formula Numero di operazioni costante
  • Difficile da ricordare
  • Numeri irrazionali

Quindi

  • per il calcolo dell’n-esimo numero di Fibonacci esistono più algoritmi con complessità molto diverse
  • al crescere di n utilizzeremo l’algoritmo più conveniente (esponenziale ⇒ iterativo ⇒ formula)