La ricerca binaria si applica agli array ordinati.
Essa controlla se l’elemento richiesto si trova nella posizione centrale dell’array altrimenti concentra la ricerca nella parte
- BASSA se ha trovato un elemento MAGGIORE
- ALTA se ha trovato un elemento MINORE
e continua finché
- non trova l’elemento,
- oppure rimane da esaminare un sottoarray vuoto.
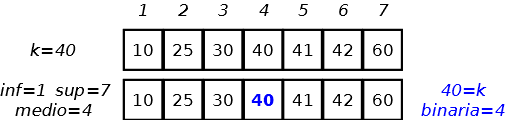 | Nel caso ottimo … l’elemento richiesto occupa la posizione centrale, basta un unico passo. |
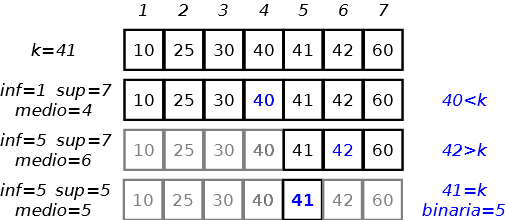 | Nel caso pessimo… sono necessari 3 passi. |
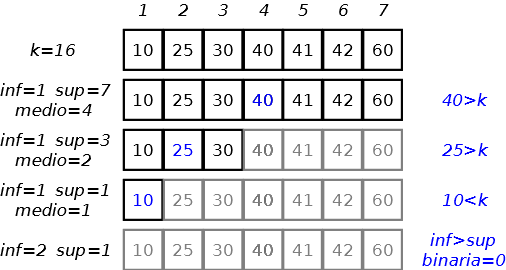 | Se l’elemento non è presente… si scopre dopo i 3 passi del caso pessimo. |
Riepilogo posizione -> passi
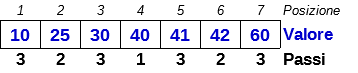
Complessità dell’algoritmo
Analizziamo il codice (Pascal)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
Function ricercaBinaria(V: Vettore; N: Integer; K: Real): Integer; Var INF , SUP , MEDIO, RISP : Integer; Begin INF :=1; SUP :=N; RISP:=0; While(INF <= SUP) And (RISP = 0) do Begin MEDIO:=(INF+SUP) Div 2; If(V[MEDIO] < K) Then INF:=MEDIO+1 Else if(V[MEDIO] = K) Then RISP:=MEDIO Else SUP:=MEDIO-1; End; ricercaBinaria:=RISP; End; |
Utilizzando la tecnica di calcolo della complessità in tempo utilizzata per la ricerca sequenziale possiamo concludere che T(x)=c1+c2x con x il numero di volte che viene eseguito il ciclo.
I calcoli approssimati per T danno
- vettore vuoto: ~7
- elemento trovato al 1° passo (in mezzo): c1+c2*1
- elemento trovato al 2° passo: c1+c2*2
- …
- elemento trovato all’ultimo passo: c1+c2*m
- elemento non presente: c1+c2*(m+1)
Supponiamo pessimisticamente di dover aspettare sempre fino all’ultimo passo, allora T(n)=c1+c2*m.
Quanto vale m?
La dimensione del vettore sul quale si effettua la ricerca passo-passo è
n > ~n/2 > ~n/4 > ~n/8 > … > n/2m > … > 2 > 1 > 0
Quando il valore della potenza di 2 a denominatore raggiunge n il ciclo termina sicuramente, cioè per
- 2m = n
- m = log2 n
quindi, nel caso pessimo T(n) = c1 + c2 m = c1 + c2 log2 n
Esempi numerici
| n | m | T(n) | |
|---|---|---|---|
| 16 | = 24 | 4 | c1+c2·4 |
| 256 | = 28 | 8 | c1+c2·8 |
| 1.024 | = 210 | 10 | c1+c2·10 |
| 65.536 | = 216 | 16 | c1+c2·16 |
| 1.048.576 | = 220 | 20 | c1+c2·20 |
| 1.073.741.824 | = 230 | 30 | c1+c2·30 |
L’algoritmo di ricerca binaria applicato a un vettore con un miliardo di elementi garantisce una risposta dopo appena 30 passi!