Congettura di Collatz – Programmare con Python

Olimpiadi Italiane di Informatica – Fase territoriale 2015

Consideriamo il seguente algoritmo, che prende in ingresso un intero positivo N:

Se N vale 1, l’algoritmo termina.
Se N è pari, dividi N per 2, altrimenti (se N è dispari) moltiplicalo per 3 e aggiungi 1.

Per esempio, applicato al valore N=6, l’algoritmo produce la seguente sequenza (di lunghezza 9, contando anche il valore iniziale N=6 e il valore finale 1): 6, 3, 10, 5, 16, 8, 4, 2, 1.
La congettura di Collatz, chiamata anche congettura 3N+1, afferma che l’algoritmo qui sopra termini sempre per qualsiasi valore N; in altri termini, se prendo un qualsiasi numero intero maggiore di 1 applicare la regola numero 2 conduce sempre al numero 1.
È riferendosi a questa celebre congettura che il famoso matematico Erdős ha commentato sul come questioni semplici ma elusive mettono in evidenza quanto poco noi si possa accedere ai misteri del “grande Libro”.
Giovanni sta cercando di dimostrare la congettura, ed è interessato alla lunghezza della sequenza. Il vostro compito è quello di aiutare Giovanni scrivendo un programma che, ricevuto in ingresso un numero N, calcoli la lunghezza della sequenza che si ottiene a partire da N.

Esempi di input/output

     +-----------+------------+
     | input.txt | output.txt |
+----+-----------+------------+
| 1° | 6         | 9          |
+----+-----------+------------+
| 2° | 24        | 11         |
+----+-----------+------------+

Olimpiadi di Informatica – Fase scolastica del 13-11-2014 – Quesito 18

Consideriamo il seguente algoritmo, che prende in ingresso un intero positivo N:

Se N vale 1, l’algoritmo termina.
Se N è pari, dividi N per 2, altrimenti (se N è dispari) moltiplicalo per 3 e aggiungi 1.

Olimpiadi di Informatica – Fase scolastica del 23-02-2021 – Quesito 18

Consideriamo il seguente algoritmo, che prende in ingresso un intero positivo N:

Se N vale 1, l’algoritmo termina.
Se N è pari, dividi N per 2, altrimenti (se N è dispari) moltiplicalo per 3 e aggiungi 1.

Vedi la discussione

1

n=int(input("n = "))

lunghezza=1;
while(n != 1):
    if(n%2 == 0):  # se n è pari si divide per 2
        n=n//2
    else:          # se n è dispari...
        n=3*n+1
    lunghezza += 1 # conta un nuovo passo

print(lunghezza)

2

Facoltativo: visualizza la sequenza da n a 1, compresi

n=int(input("n = "))
print(n, end=' ')      # Visualizza il numero di partenza

lunghezza=1;
while(n != 1):
    if(n%2 == 0):
        n=n//2
    else:
        n=3*n+1
    print(n, end=' ')  # visualizza il risultato dell'algoritmo
    lunghezza += 1 

print()
print(lunghezza)

Versione OII

f=open("input.txt", "r")
n=int(f.read())
f.close()

lunghezza=1;
while(n != 1):
    if(n%2 == 0):
        n=n//2
    else:
        n=3*n+1
    lunghezza += 1 

f=open("output.txt", "w")
f.write(str(lunghezza))
f.close()

Quesito 2

NUM è il numero da 10 a 20 con lunghezza minima LUN

def lunghezza(n):
    conto=1
    while(n != 1):
        if(n%2 == 0):
            n=n//2
        else: 
            n=3*n+1
        conto+=1
    return conto

PRIMO =10 
ULTIMO=20 
NUM=0
LUN=1000 # esagerato...

for num in range(PRIMO,ULTIMO+1):
    lun=lunghezza(num)
    if(lun < LUN):
        NUM=num
        LUN=lun
    print(num,lun)  # facoltativo

print(NUM,':',LUN)

matplotlib

La sequenza per n=167

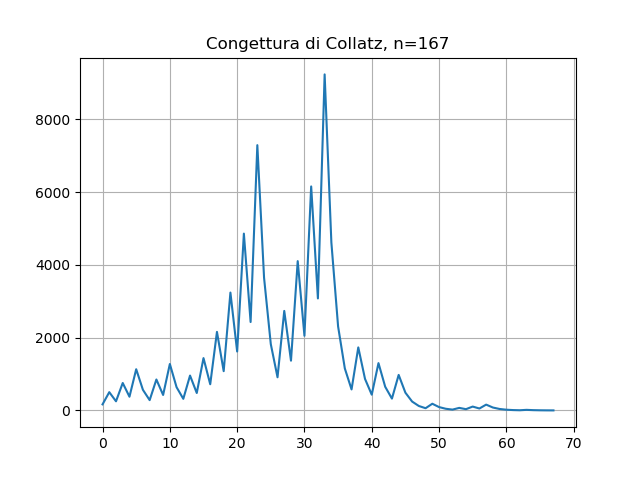
import matplotlib.pyplot as plt
 
n=167
N=[]
N.append(n)
while(n != 1):
    if(n%2 == 0):
        n=n//2
    else: 
        n=3*n+1
    N.append(n)

plt.grid(which="major")
plt.plot(N)
plt.title("Congettura di Collatz, n=167")
plt.show()

Lunghezze per n da 10 a 20

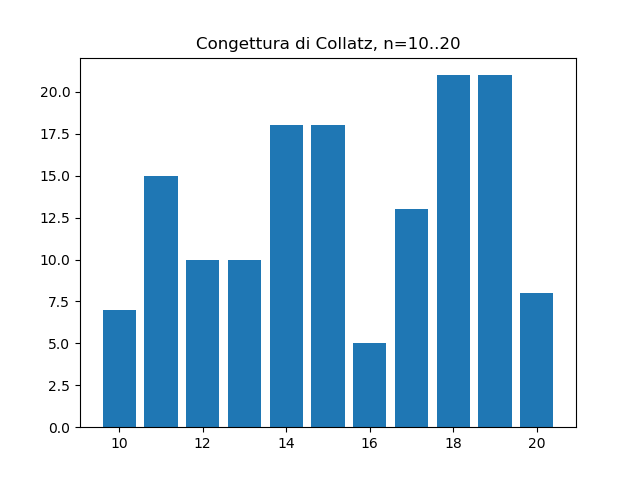
Lunghezze per n da 48 a 52

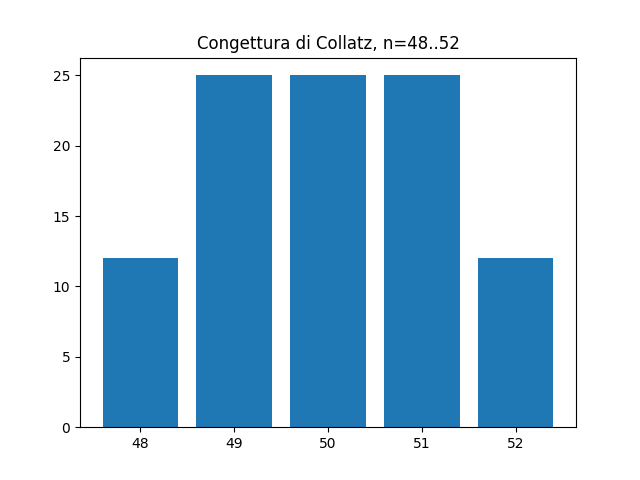
import matplotlib.pyplot as plt
import math
 
def lunghezza(n): 
    conto=1 
    while(n != 1): 
        if(n%2 == 0): 
            n=n//2 
        else: 
            n=3*n+1 
        conto+=1 
    return conto 

PRIMO =10  # 48
ULTIMO=20  # 52

x=range(PRIMO,ULTIMO+1)
y=[]

NUM=0
LUN=math.inf
for num in x:
    lun=lunghezza(num)
    print(num,lun)
    y.append(lun)
    if(lun < LUN):
        NUM=num
        LUN=lun        

print("-->",NUM,LUN)
    
plt.bar(x,y)
plt.title("Congettura di Collatz, n=10..20")
plt.show()

Da 1 a 100 (1000)

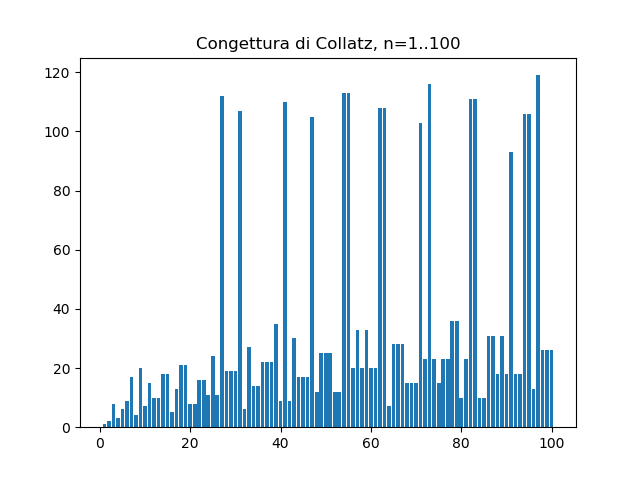
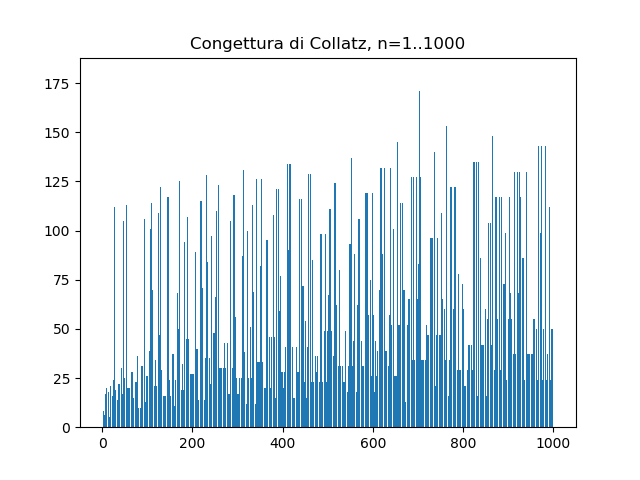
import matplotlib.pyplot as plt
 
def lunghezza(n):
    conto=1
    while(n != 1):
        if(n%2 == 0):
            n=n//2
        else: 
            n=3*n+1
        conto+=1
    return conto

PRIMO =1 
ULTIMO=100               # 1000 
x=range(PRIMO,ULTIMO+1)
y=[]
for n in x:
    lun=lunghezza(n)
    print(n,lun) # facoltativo
    y.append(lun)
    
plt.bar(x,y)
plt.title("Congettura di Collatz, n=" + str(PRIMO) + ".." + str(ULTIMO))
plt.show()