Pesca bizzarra

Pinco Panco e Panco Pinco hanno deciso di andare a pesca di ostrichette, ciascuno con la propria barca.
Poiché sanno solo andare in direzione Nord o in direzione Est, Pinco Panco e Panco Pinco decidono di dividere concettualmente la zona di pesca in quadrati adiacenti, con i lati nelle direzioni Nord-Sud e Est-Ovest, ossia disposti come in un foglio a quadretti, e numerati secondo le coordinate cartesiane intere.
Pertanto, ogni quadrato della griglia è univocamente identificato da una coppia di interi (I,J), ossia è collocato all’incrocio della colonna I e della riga J nella suddetta divisione (dove 1 <= I < 231 e 1 <= J < 231).

Ciascuna barca si muove soltanto in due direzioni, attraverso uno dei seguenti comandi numerici, che vengono inviati da una base a terra:

• +D (=Nord) per spostarsi dal quadrato attualmente occupato (I,J) al quadrato (I, J+D) attraversando tutti i D-1 quadrati intermedi sulla colonna I, dove D è un intero positivo;
• -D (=Est) per spostarsi dal quadrato attualmente occupato (I,J) al quadrato (I+D, J) attraversando tutti i D-1 quadrati intermedi sulla riga J, dove D è un intero positivo;

Una sequenza di comandi è quindi una sequenza di interi diversi da zero che termina con zero.

Pinco Panco e Panco Pinco utilizzano lo stesso quadrato A=(I₀,J₀) di partenza: i loro sistemi di navigazione sono sincronizzati e ogni barca riceve dalla base a terra la propria sequenza di comandi con la garanzia che i quadrati attraversati da entrambe le barche sono solo quello di partenza A e quello di arrivo B.
Soltanto alcuni dei quadrati sono pescosi e la base a terra è a conoscenza della loro posizione.

Entrambe le barche iniziano quindi il percorso dal quadrato di partenza A=(I₀,J₀) e ciascuna viene pilotata con la corrispondente sequenza di comandi.
Durante il percorso, ciascuna barca prende un’estremità di un’enorme rete da pesca (ebbene sì, Pinco Panco e Panco Pinco usano la rete per pescare le ostrichette!).
Le due estremità dovranno essere ricongiunte nel quadrato di arrivo B: in questo modo, verranno catturate tutte le ostrichette che si troveranno nella zona racchiusa dall’enorme rete.

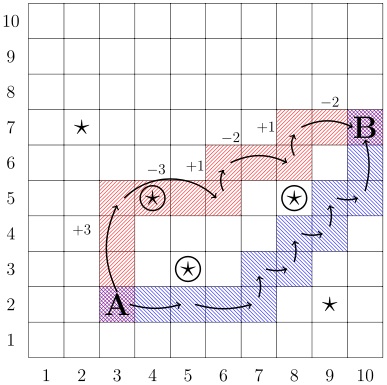
Per esempio, siano I₀=3 e J₀=2.
Nella figura, i P=5 quadrati con un asterisco sono pescosi e i quadrati colorati indicano quelli percorsi delle due barche, con le sequenze di comandi +3 -3 +1 -2 +1 -2 0 e -2 -2 +1 -1 +1 -1 +1 -1 +2 0 (notare che possono esserci più numeri consecutivi dello stesso segno).
Risultano Q=3 quadrati pescosi nella zona delimitata dalla rete (quelli identificati da (4,5), (5,3) e (8,5)).

Aiuta Pinco Panco e Panco Pinco a calcolare il numero Q di quadrati pescosi che saranno inglobati dalla rete in questo modo.
In tale conteggio, vanno considerati anche i quadrati attraversati dalle due barche.

Dati in Input

Il file input.txt è composto da P+4 righe, dove P è il numero totale di quadrati pescosi.

• La prima riga contiene un intero P per indicare che la zona di pesca contiene P quadrati pescosi.
• La seconda riga contiene due interi I₀ e J₀ separati da uno spazio, per indicare che il quadrato di partenza è (I₀, J₀).
• Le successive P righe contengono le coordinate dei P quadrati pescosi. Ogni riga è composta da due interi I e J separati da uno spazio (dove 1 <= I < 231 e 1 <= J < 231), per indicare che quel quadrato pescoso ha coordinate (I, J).
• La penultima riga contiene una sequenza di interi diversi da 0 e terminata da uno 0, separati da uno spazio: rappresenta la prima sequenza di comandi (dove 0 è semplicemente utilizzato per indicare la fine della sequenza di interi).
• L’ultima riga contiene anch’essa una sequenza di interi diversi da 0, terminata da zero, separati da uno spazio: rappresenta la seconda sequenza di comandi.

 

Dati in Output

Il file output.txt è composto da una sola riga contenente il numero Q di quadrati pescosi che sono inglobati dalla rete.

Assunzioni

• 1 <= P <= 1000000
• 1 <= I₀ < 2³¹
• 1 <= J₀ < 2³¹
• Una sequenza di comandi contiene M interi diversi da 0, per un qualche valore 2 <= M <= 1000000.

 

Esempi