Calcolare la probabilità che in un gruppo di persone ci sia almeno una coincidenza di compleanni.
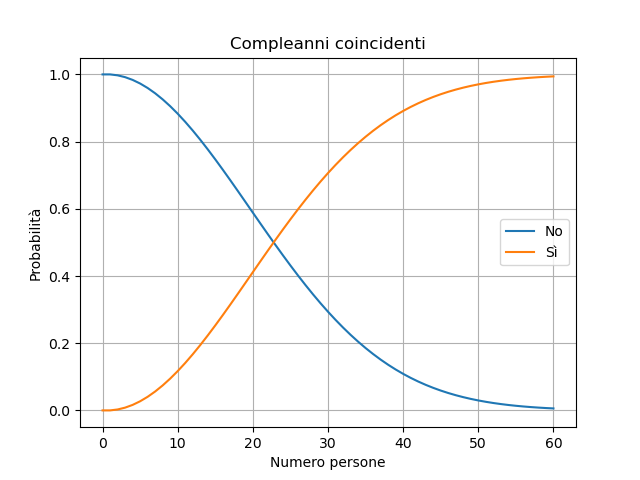
Osserva l’andamento della probabilità al crescere di n
Nel grafico compaiono gli andamenti di probabilità dei due eventi complementari
- “No, nessuna coppia di compleanni coincidenti”.
- “Sì, almeno una coppia di compleanni coincidenti”
Ecco i valori per n=1..25 (calcolati con Python secondo la discussione 1)
+----+----------+
| 0 | 0.000000 |
| 1 | 0.000000 |
| 3 | 0.008204 |
| 4 | 0.016356 |
| 5 | 0.027136 |
| 6 | 0.040462 |
| 7 | 0.056236 |
| 8 | 0.074335 |
| 9 | 0.094624 |
| 10 | 0.116948 |
| 11 | 0.141141 |
| 12 | 0.167025 |
| 13 | 0.194410 |
| 14 | 0.223103 |
| 15 | 0.252901 |
| 16 | 0.283604 |
| 17 | 0.315008 |
| 18 | 0.346911 |
| 19 | 0.379119 |
| 20 | 0.411438 |
| 21 | 0.443688 |
| 22 | 0.475695 |
| 23 | 0.507297 |
| 24 | 0.538344 |
| 25 | 0.568700 |
+----+----------+
Per n=23 la probabilità è superiore al 50%
Quesiti di provenienza diversa, in ordine alfabetico
Qual è la probabilità che in una classe di 25 alunni, almeno due compiano gli anni lo stesso giorno?
RISORSE ONLINE