Esame di Stato 2012 PNI – 5

di

Siano dati nello spazio n punti P1, P2, P3, …, PN.
Quanti sono i segmenti che li congiungono a due a due?
Quanti i triangoli che hanno per vertici questi punti (supposto che nessuna terna sia allineata)?
Quanti i tetraedri (supposta che nessuna quaterna sia complanare)?

Osserva

  1. Con una coppia di punti diversi determini un unico segmento.
    Quante coppie ordinate con n punti?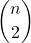 \displaystyle {n \choose 2}
  2. Con una terna di punti diversi determini un unico triangolo.
    Quante terne ordinate con n punti?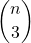 \displaystyle {n \choose 3}
  3. Con una quaterna di punti diversi determini un unico tetraedo.
    Quante quaterne ordinate con n punti?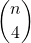 \displaystyle {n \choose 4}

Esercizio

nSegmentiTriangoliTetraedi
1———
000
2P1P2 ——
\displaystyle {2 \choose 2} = 100
3P1P2 – P1P3 – P2P3P1P2P3 —
\displaystyle {3 \choose 2} = 3\displaystyle {3 \choose 3} = 10
4P1P2 – P1P3 – P1P4 – P2P3 – P2P4 – P3P4 P1P2P3 – P1P2P4 – P1P3P4 – P2P3P4P1P2P3P4
\displaystyle {4 \choose 2} = 6\displaystyle {4 \choose 3} = 4\displaystyle {4 \choose 4} = 1
5P1P2 – P1P3 – P1P4 – P1P5 – P2P3 – P2P4
P2P5 – P3P4 – P3P5 – P4P5 		P1P2P3 – P1P2P4 – P1P2P5 – P1P3P4
P1P3P5 – P1P4P5 – P2P3P4 – P2P3P5
P2P4P5 – P3P4P5 		P1P2P3P4 – P1P2P3P5
P1P2P4P5 – P1P3P4P5
P2P3P4P5
\displaystyle {5 \choose 2} = 10\displaystyle {5 \choose 3} = 10\displaystyle {5 \choose 4} = 5
6… … …
\displaystyle {6 \choose 2} = 15\displaystyle {6 \choose 3} = 20\displaystyle {6 \choose 4} = 15