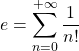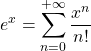Numero di Eulero

di

Wikipedia

In matematica il simbolo e denota una costante molto importante per via delle sue applicazioni in diversi campi.

Poiché e corrisponde ad un numero irrazionale (in particolare ad uno trascendente), non è esprimibile come frazione o come numero decimale periodico.

La sua espressione con 55 cifre decimali è

2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749.

In ambito internazionale il numero e è chiamato numero di Eulero, in Italia talvolta anche numero di Nepero.

Il numero di Eulero è collegato con la funzione esponenziale, che associa ad un numero reale x il numero dato dalla potenza e^x, e con la funzione logaritmo naturale (la funzione inversa dell’esponenziale).

Montante

…

Imparare le cifre a memoria?

…

Formule notevoli

Il numero di Eulero, come pi greco, compare in molte formule notevoli

  • \displaystyle e=\lim_{n \rightarrow +\infty}\left(1+\frac{1}{n}\right)^n
  • \displaystyle e^x=\lim_{n \rightarrow +\infty}\left(1+\frac{x}{n}\right)^n
  • \displaystyle e=\sum_{n=0}^{+\infty}\frac{1}{n!}
  • \displaystyle e^x=\sum_{n=0}^{+\infty}\frac{x^n}{n!}
  • e^{i x}=\cos x +i \sin x
  • e^{i \pi}+1=0
  • \displaystyle \frac{\partial e^x}{\partial x}= e^x
  • \displaystyle\int e^x\ dx = e^x + c
  • \displaystyle\int_{0}^{+\infty}\,e^{-x^2}\,dx=\sqrt{\frac{\pi}{4}}
  • \displaystyle\int_{-\infty}^{+\infty}\,e^{-x^2}\,dx=\sqrt{\pi}
  • \displaystyle \int_{-\infty}^{+\infty}\,e^{-\frac{x^2}{2}}\,dx=\sqrt{2\pi}
  • \displaystyle f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2 {\sigma}^2}}
  • \displaystyle n!\approx \sqrt{2 \pi n} \left( \frac{n}{e} \right)^{n}

Approfondimenti