Si consideri la variabile “spesa mensile” osservata su tre famiglie nel corso del 2018.
La famiglia A spende in media 1000 euro al mese, con una varianza di 200 euro².
La famiglia B spende ogni mese 8/10 della spesa della prima.
La famiglia C spende ogni mese esattamente 200 euro al mese in meno della prima.
Come saranno le medie e le varianze delle spese mensili delle famiglie B e C?
- Le medie della famiglia B e C coincidono: 800 euro.
La varianza delle spese mensili per la famiglia B è 128 euro² e per la famiglia C è 0 - Le medie della famiglia B e C coincidono: 800 euro.
La varianza delle spese mensili per la famiglia B è 128 euro² e per la famiglia C non varia rispetto alla famiglia A - Per la famiglia B, la media è 800 euro e la varianza 128 euro².
La media e la varianza della famiglia C sono identiche rispetto a quelle della famiglia A - Con i dati a disposizione non posso calcolare la media e varianza per le famiglie B e C
- Non so
Fai tutti i passi, senza utilizzare direttamente le proprietà della media e della varianza
Calcoli per la media
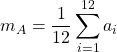 = 1000
= 1000
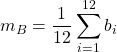
= 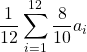 =
= 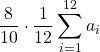 =
= ![]() =
= ![]() = 800
= 800
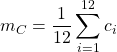
= 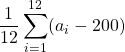 =
= 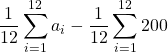 =
= ![]() =
= ![]() = 800
= 800
Calcoli per la varianza
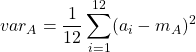 = 200
= 200
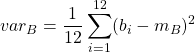
= 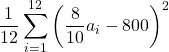 =
= 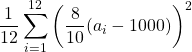 =
= 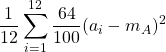 =
= 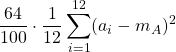 =
= ![]() =
= ![]() = 128
= 128
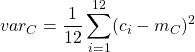
= 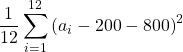 =
= 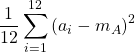 =
= ![]() = 200
= 200
