A ogni passo si costruiscono i due poligoni simili, inscritto e circoscritto, e si calcolano i corrispondenti perimetri
![]()
![]()
…
![]()
Si divide per ![]()
![]()
si ottengono due nuove approssimazioni di π, per difetto e per eccesso
![]()
Primo passo
- Un esagono inscritto e un esagono circoscritto
- Δ è la differenze tra i 2 apotemi necessaria per il passo successivo.
| Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| Esagono inscritto | 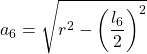 | ||||
| Esagono circoscritto |
Passi successivi
- Un poligono inscritto e un poligono circoscritto
- Il numero di lati è doppio rispetto al passo precedente
| Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| Esagono inscritto | 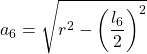 | ||||
| Poligono inscritto | 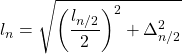 | 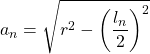 | |||
| Esagono circoscritto | |||||
| Poligono circoscritto |
Approssimazioni formali
| Passo | #Lati | ||
|---|---|---|---|
| 1 | 6 | ||
| 2 | 12 | 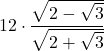 | |
| 3 | 24 | 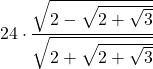 | |
| 4 | 48 | 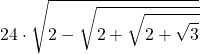 | 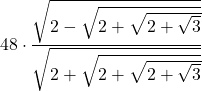 |
| 5 | 96 | 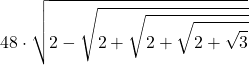 | 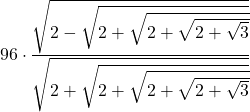 |
| 6 | 192 | … | … |
Approssimazioni numeriche
| Passo | #Lati | ||
|---|---|---|---|
| 1 | 6 | 3.0000000000 | 3.4641016151 |
| 2 | 12 | 3.1058285412 | 3.2153903092 |
| 3 | 24 | 3.1326286133 | 3.1596599421 |
| 4 | 48 | 3.1393502030 | 3.1460862151 |
| 5 | 96 | 3.1410319509 | 3.142714996 |
| 6 | 192 | 3.1414524723 | 3.1418730500 |
| 7 | 384 | 3.1415576079 | 3.1416627471 |
| 8 | 768 | 3,1415838921 | 3,1416101766 |
| 9 | 1536 | 3,1415904632 | 3,1415970343 |
| 10 | 3072 | 3,1415921060 | 3,1415937488 |
| 11 | 6144 | 3,1415925167 | 3,1415929274 |
| 12 | 12288 | 3,1415926194 | 3,1415927220 |
| 13 | 24576 | 3,1415926450 | 3,1415926707 |
| 14 | 49152 | 3.1415926515 | 3.1415926579 |
| 15 | 98304 | 3.1415926531 | 3.1415926547 |