Da Wikipedia
Il metodo di esaustione è un procedimento utile a calcolare aree di varie figure geometriche piane.
Consiste nella costruzione di una successione di poligoni che convergono alla figura data.
L’area della figura risulta essere quindi il limite delle aree dei poligoni.Il sofista Antifonte (430 a.C.) tentò di determinare l’area del cerchio inscrivendovi dei triangoli sempre più piccoli, fino a quando la sua area non “esaurisce”.
Un più famoso esempio di applicazione del metodo di esaustione è quello della quadratura del cerchio effettuata da Archimede.
Il primo poligono è un esagono inscritto.
Il poligono successivo ha il doppio dei lati del precedente.
Si ottiene un’approssimazione sempre più precisa di pi greco considerando che
![]()
![]()
![]()
- Facciamo 3 passi
 è necessario per il passo successivo
è necessario per il passo successivo
Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| 6 | 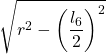 | ||||
| 12 | 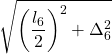 | 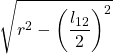 | |||
| 24 | 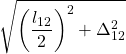 | 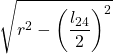 |
- Sostituendo
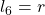
Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| 6 | |||||
| 12 | |||||
| 24 | 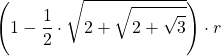 |
- L’approssimazione di
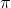 non dipende da
non dipende da 
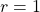
Lato | Perimetro | Pi greco | Apotema | Delta | |
|---|---|---|---|---|---|
| 6 | 1 | 6 | 3 | ||
| 12 | |||||
| 24 | |||||
| 48 | 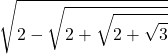 | 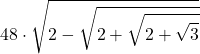 | 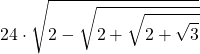 | 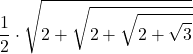 | 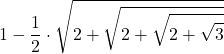 |
Approssimazioni
| Passo | #Lati | ||
|---|---|---|---|
| 1 | 6 | 3,0000000000 | |
| 2 | 12 | 3,1058285412 | |
| 3 | 24 | 3,1326286133 | |
| 4 | 48 | 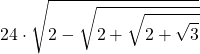 | 3,1393502030 |
| 5 | 96 | 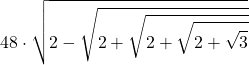 | 3,1410319509 |
| 6 | 192 | 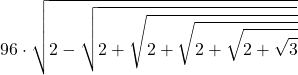 | 3,1414524723 |
| 7 | 384 | … | 3,1415576079 |
| 8 | 768 | … | 3,1415838921 |
| 9 | 1536 | … | 3,1415904632 |
| 10 | 3072 | … | 3,1415921060 |
| 11 | 6144 | … | 3,1415925167 |
| 12 | 12288 | … | 3,1415926194 |
| 13 | 24576 | … | 3,1415926450 |
| 14 | 49152 | … | 3,1415926515 |
| 15 | 98304 | … | 3,1415926531 |