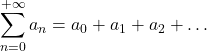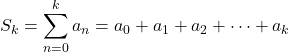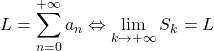Da Wikipedia
Una successione è una sequenza ordinata di infiniti elementi.
Una serie è la somma degli elementi di una successione.
Si tratta di una generalizzazione dell’operazione di addizione, che può essere in tal modo estesa al caso in cui partecipano infiniti termini.
Si consideri una successione di elementi:
Si definisce serie associata a
la somma formale
Per ogni indice k della successione si definisce la somma parziale (o ridotta)
come la somma dei termini della successione
da 0 a k.
Si dice che la serie
tende o converge al limite L se la successione delle somme parziali
associata converge a L.
Ovvero
Questo limite si dice somma della serie.
Serie notevoli
| 1 | = 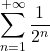 | = | = | Reciproci delle potenze di 2 |
| 1 | = 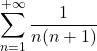 | = | = | … |
= 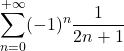 | = | = | Leibniz Reciproci dei numeri dispari, con segni alterni | |
= 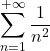 | = | = | Eulero Reciproci dei quadrati | |
= 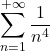 | = | = | Reciproci delle 4° potenze | |
| e | = | = | = | Reciproci dei fattoriali |
= 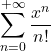 | … | … | Rapporti tra le potenze e i fattoriali | |
| … | … | … | … | … |
RISORSE
- Wikipedia: Serie
- Wikipedia: Srinivasa Ramanujan (serie sorprendenti…)