Il grafo dei collegamenti bidirezionali fra 7 nodi (n1, n2, …, n7) è descritto da una tabella
nodo1 nodo2 distanza in km n1 n2 140 n2 n3 180 n2 n4 100 n1 n4 120 n2 n5 65 n4 n5 170 n4 n6 230 n3 n7 150 n5 n7 160 n7 n6 90 Trovare la lista L del percorso più breve dal nodo n1 al nodo n7 e calcolarne la distanza D in chilometri.
Soluzione: L=[n1, n2, n5, n7], D=365.
Soluzione
Disegno il grafo corrispondente alla tabella e individuo la soluzione passo-passo
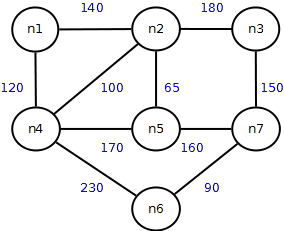
Distanze minime tra n1 e le città immediatamente vicine (n2 e n4)
n1 -> n2 = 140
n1 -> n4 = 120
n1 -> n4 = 120
Distanze minime tra n1 e le città immediatamente vicine a n2 e n4 (n3, n5, n6)
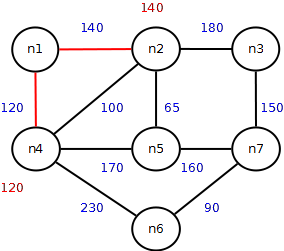
n1 -> n2 = 140
n1 -> n2 -> n3= 320
n1 -> n4 = 120
n1 -> n2 -> n4= 240, scartata
n1 -> n2 -> n5= 205
n1 -> n4 -> n5= 290, scartata
n1 -> n4 -> n6 = 350
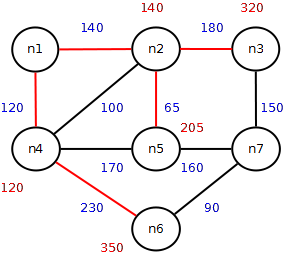
Distanza minima tra n1 e la città immediatamente vicina a n3, n5, n6 (n7)
n1 -> n2 = 140
n1 -> n2 -> n3= 320
n1 -> n4 = 120
n1 -> n2 -> n5= 205
n1 -> n4 -> n6 = 350
n1 -> n2 -> n5 -> n7 = 365
n1 -> n2 -> n3 -> n7 = 470, scartata
n1 -> n4 -> n6 -> n7 = 440, scartata
n1 -> n2 -> n3= 320
n1 -> n4 = 120
n1 -> n2 -> n5= 205
n1 -> n4 -> n6 = 350
n1 -> n2 -> n5 -> n7 = 365
n1 -> n2 -> n3 -> n7 = 470, scartata
n1 -> n4 -> n6 -> n7 = 440, scartata
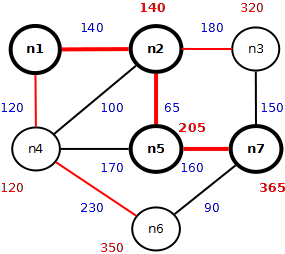
I grafi illustrano i passaggi risolutivi ma sono superflui rispetto ai calcoli algebrici.