Sono date 4 città A, B, C, D e le distanze che le separano attraverso un collegamento diretto sono espresse dalla seguente matrice quadrata:
A B C D A 0 5 4 3 B 5 0 1 2 C 4 1 0 3 D 3 2 3 0 Ad esempio
- l’elemento di riga A e colonna B esprime il fatto che la distanza fra A e B utilizzando il collegamento diretto fra le città è pari a 5;
- analogamente si può verificare che la distanza del collegamento diretto fra D e C è pari a 3.
Qual è la lunghezza complessiva del percorso più breve che partendo da A visita tutte le altre città senza passare nuovamente per A?
Ad esempio,
- se andiamo da A a B e poi da B a C e infine da C a D, la lunghezza complessiva del percorso è pari a 9
infatti 5, 1 e 3 sono le distanze dei tre collegamenti.
Risposta: 6.
Soluzione #1
Partendo da A possiamo arrivare a D (costo 3) poi a B (costo 2) e infine a C (costo 1).
A questo punto abbiamo raggiunto tutte le città con costo 3+2+1=6.Possiamo inoltre verificare che non esiste un percorso complessivo più breve (ad esempio di lunghezza 5 o meno).
Soluzione #2
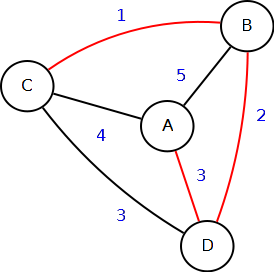Rappresento graficamente i collegamenti esistenti.
Realizzo un percorso completo partendo dai collegamenti più brevi…
Ho toccato tutte le città utilizzando il percorso più breve perché ho utilizzato i collegamenti con distanza minima!
Soluzione #3
Seguo i passi
- considero tutti i percorsi possibili
- per ognuno calcolo la lunghezza complessiva
- individuo il percorso con la lunghezza minima.
Osserva
| Percorso | Lunghezza | ||
|---|---|---|---|
| 1 | ABCD | 5+1+3 | 9 |
| 2 | ABDC | 5+2+3 | 10 |
| 3 | ACBD | 4+1+2 | 7 |
| 4 | ACDB | 4+3+2 | 9 |
| 5 | ADBC | 3+2+1 | 6 |
| 6 | ADCB | 3+3+1 | 7 |
Concludo: il 5° percorso (ADBC) ha la distanza complessiva minima (6).