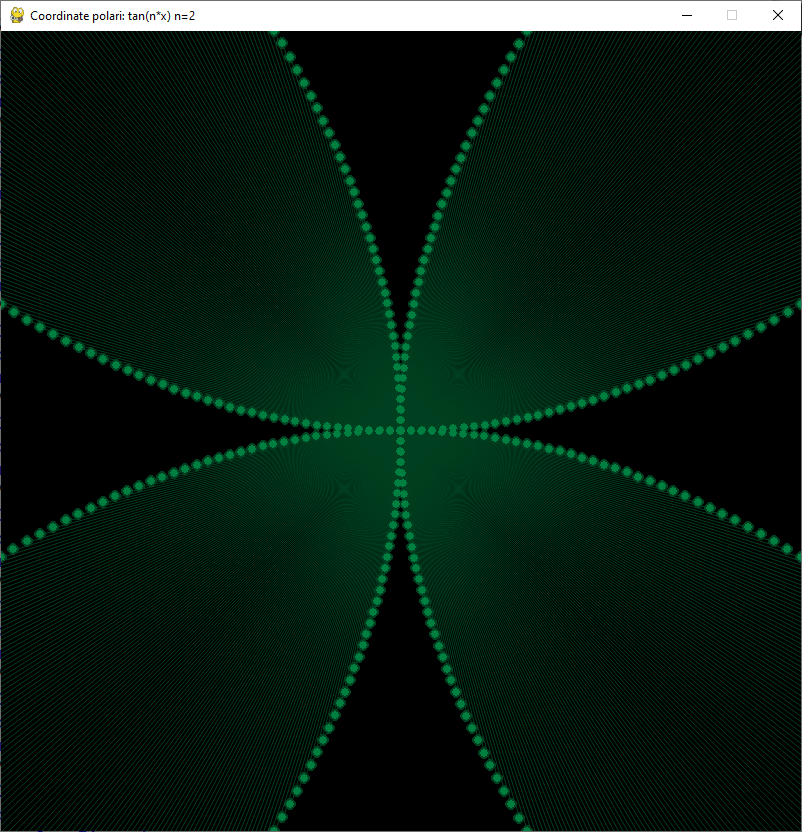
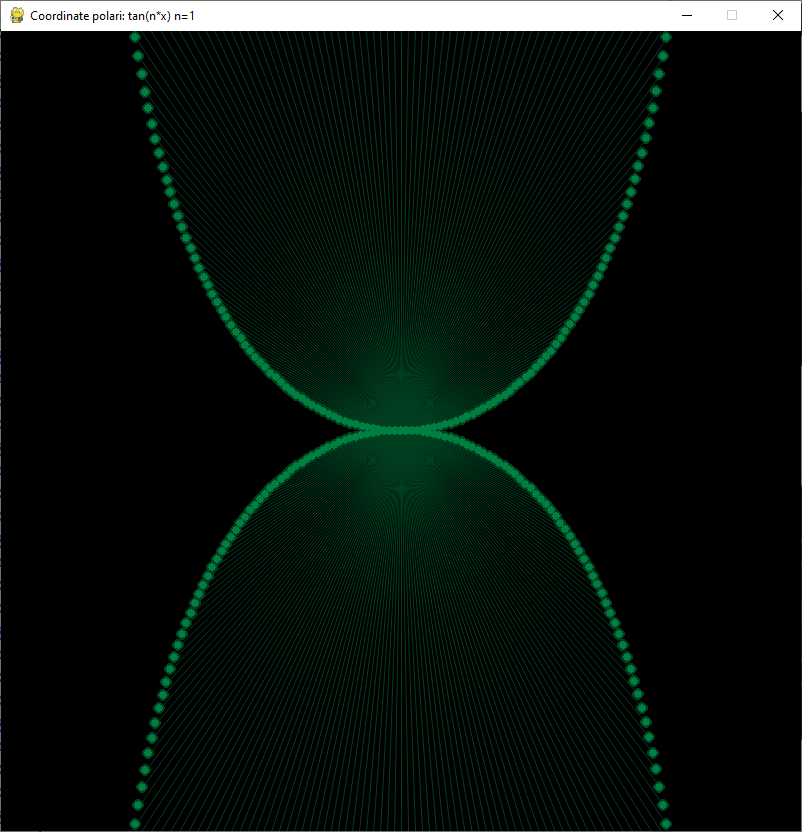
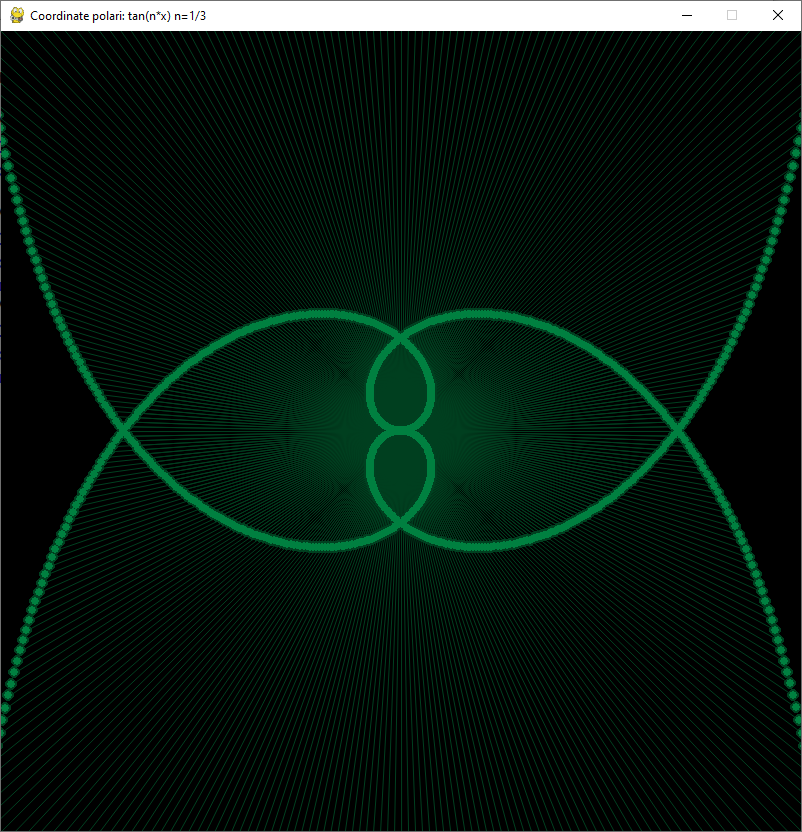
Disegna per punti una circonferenza calcolando le coordinate x,y corrispondenti ad ogni angolo da 0° a 360°

Nella parte iniziale del codice è presente una funzione costante che rappresenta la distanza del punto della circonferenza dal centro della circonferenza: cambiando questa funzione si ottengono le diverse figure in coordinate polari!
def f(x): return 1
Sono presenti altri parametri per adattare la figura alla finestra o per migliorare il suo aspetto
DIM = 800 # Dimensione della finestra grafica
RAGGIO = 0.4*DIM # Fattore di scala
GIRI = 1 # Giri completi da compiere
dAngolo = 1 # Angolo tra due punti notevoli, risoluzione
...
...import math
import pygame
def f(x): return 1
TITOLO ="Coordinate polari: f(x)=1"
DIM =800
RAGGIO =0.4*DIM # Fattore di scala
raggio1=6
raggio2=4
GIRI =1 # Giri completi
dAngolo=1 # angolo tra due punti notevoli
FRAME =60
COLOR1 =(0, 64, 32)
COLOR2 =(0,128, 64)
WIDTH =DIM # Larghezza
HEIGHT =DIM # Altezza
W2 =WIDTH/2
H2 =HEIGHT/2
centro =(W2, H2) # Centro dello schermo
NUMERO =360*GIRI
PUNTI =[] # Sequenza dei punti notevoli
pygame.init()
screen=pygame.display.set_mode((WIDTH, HEIGHT))
pygame.display.set_caption(TITOLO)
clock=pygame.time.Clock()
angolo=0
while angolo < NUMERO:
phi=math.radians(angolo)
ro =f(phi)
x =W2+ro*RAGGIO*math.cos(phi)
y =H2-ro*RAGGIO*math.sin(phi)
angolo += dAngolo
punto=(x,y)
PUNTI.append(punto)
pygame.draw.aaline(screen, COLOR1, centro, punto )
pygame.draw.circle(screen, COLOR1, punto , raggio1)
pygame.display.flip()
clock.tick(FRAME)
for punto in PUNTI:
pygame.draw.circle(screen, COLOR2, punto, raggio2)
pygame.display.flip()
input("Premi INVIO per chiudere la finestra...")
pygame.quit()Nelle prossime pagine sarà sufficiente modificare la funzione e adattare RAGGIO e GIRI secondo le necessità
Spirali



Curve rodonee – 1
![]()






Curve rodonee – 2
![]()






Curve rodonee – 3
![]()


Curve rodonee – 4
![]()


Reciproco del coseno
![]()


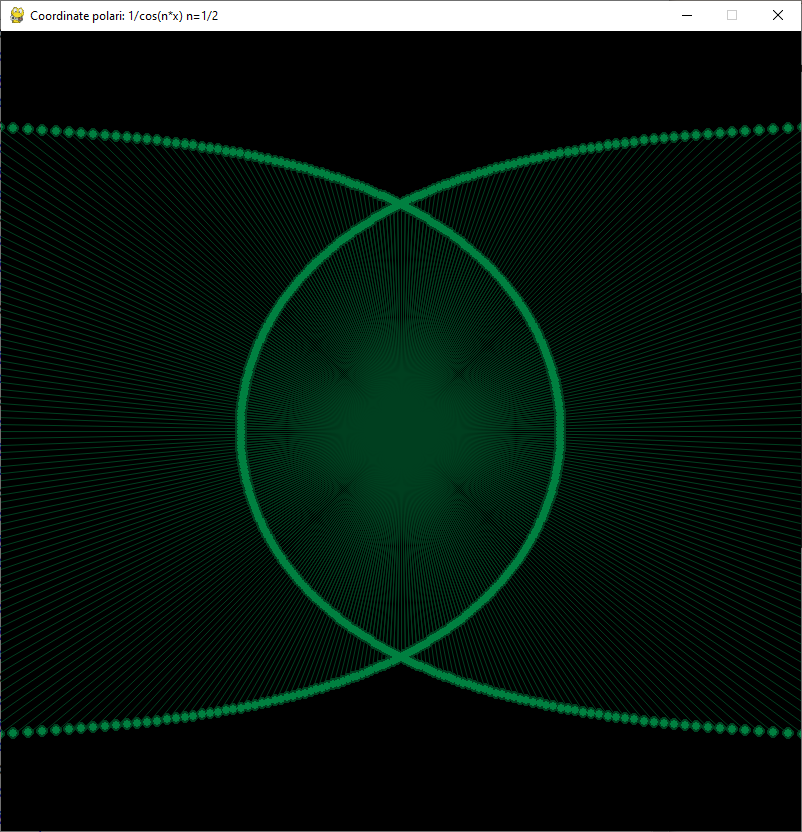

Funzione tangente
![]()