Problema 1 – Stringhe Trine
Una stringa si dice trina se è della forma aaa, ovvero se è composta da tre parti uguali.
Si scriva un programma che, ricevuta in ingresso una stringa sull’alfabeto {a, b, c}, lasci sul nastro al termine della computazione la stringa trina ottenuta triplicando la stringa di ingresso.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| a | aaa |
| abc | abcabcabc |
| babba | babbababbababba |
| ccc | ccccccccc |
Problema 2 – Numeri Trini
Un numero intero si dice trino se è divisibile per 3. Se n è trino, n+1 si dicestrino e n+2 distrino.
Si scriva un programma che, dato in input un numero decimale, lasci sul nastro una delle tre stringhe TRINO, STRINO o DISTRINO a seconda dei casi.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 3 | TRINO |
| 5 | DISTRINO |
| 82 | STRINO |
| 0 | TRINO |
Problema 3 – Strinatura di numeri
Si scriva un programma che, dato in ingresso un numero decimale, lasci sul nastro il numero strino più vicino.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 24 | 25 |
| 2 | 1 |
| 0 | 1 |
| 91 | 91 |
Problema 4 – Inserimento ordinato
Sia data sul nastro una singola cifra decimale, seguita da una X e quindi da una sequenza di cifre decimali di lunghezza qualunque (anche 0).
Si scriva il programma di una macchina di Turing che inserisca il numero dato nella sequenza in modo ordinato, lasciando sul nastro la sequenza risultante.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 5X127 | 1257 |
| 1X0000111117777999 | 00001111117777999 |
| 3X | 3 |
| 4X134 | 1344 |
| 1X133334 | 1133334 |
Problema 5 – Intersomma progressiva
L’intersomma di un numero decimale è la somma aritmetica delle cifre che lo compongono.
- Per esempio, l’intersomma di 186 è 1+8+6 ovvero 15.
- Ovviamente, è possibile calcolare l’intersomma del risultato, in questo caso 1+5 ovvero 6.
Si scriva un programma che, ricevuto in ingresso un numero decimale, restituisca l’intera sequenza ottenuta applicando ripetutamente l’operazione di intersomma al numero di ingresso, fino a che il risultato non è costituito da una sola cifra.
I valori nella sequenza devono essere separati da spazi.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 186 | 186 15 6 |
| 2500 | 2500 7 |
| 594326 | 594326 29 11 2 |
| 1 | 1 |
| 100000 | 100000 1 |
| 0 | 0 |
Problema 6 – Contafoglie
Un grafo è una struttura dati formata da un certo numero di nodi connessi da archi.
Un tipo particolarmente importante di grafo è l’albero, caratterizzato dal fatto che ogni nodo può essere connesso a 0 o più figli.
I nodi senza figli sono detti foglie.
Tutti i nodi hanno esattamente un padre, ad eccezione del nodo alla base, detto radice, che è l’unico a non avere padre.
Gli alberi in Informatica crescono al contrario che in Natura, e sono normalmente rappresentati con la radice in alto e le foglie in basso, come negli esempi illustrati più sotto.
Per rappresentare un albero come una stringa è possibile usare le parentesi per indicare la relazione padre-figlio, e singole cifre decimali per indicare le foglie.
Per esempio, (2 3) rappresenta un albero con una radice e due foglie contenenti i valori 2 e 3.
L’albero ((1 2) 3) invece ha un nodo a sinistra che ha come figli due foglie (1 e 2) e un altro figlio foglia (valore 3).
| ALBERO | RAPPRESENTAZIONE |
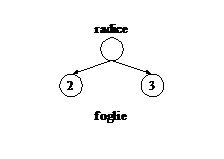 | (2 3) |
|---|---|
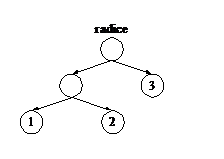 | ((1 2) 3) |
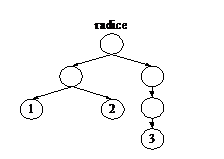 | ((1 2) ((3))) |
Più in generale nei nostri alberi le parentesi introducono un nodo intermedio nell’albero i cui figli possono essere:
- Un nuovo nodo intermedio
- Una foglia (una cifra compresa tra 0 e 9).
Si scriva il programma di una macchina di Turing che, dato un albero sul nastro (codificato come descritto e senza spazi intermedi), scriva il numero di foglie in esso presenti.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 2 | 1 |
| (12) | 2 |
| ((((1)2)(23))(111)) | 7 |
| (1) | 1 |
| ((1)) | 1 |
| ((2)(4)(6)(123456789)) | 12 |
Problema 7 – Profondità di un albero
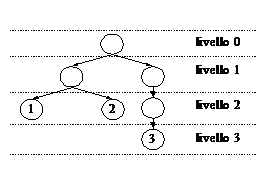
Come visibile negli esempi dell’esercizio precedente, un albero è tipicamente organizzato per livelli, dati dal numero di nodi che si incontrano partendo dalla radice per arrivare a un nodo dato.
Per esempio, i livelli dell’albero ((12)((3)) sono descritti nella figura seguente:
Si scriva il programma di una macchina di Turing che, data sul nastro la definizione di un albero, ne calcoli la profondità, ovvero il numero di livelli massimo dell’albero.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 9 | 1 |
| (12) | 2 |
| ((12)3) | 3 |
| ((12)((3))) | 4 |
| ((43563)(2(1))) | 4 |
Problema 8 – Diametro di un albero
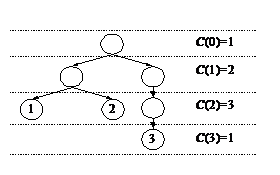
Si definisce C(l) la cardinalità del livello l di un albero il numero di nodi di quel livello.
Si scriva il programma di una macchina di Turing che, dato un albero sul nastro, scriva la cardinalità massima dell’albero, ovvero il più grande valore di C(l) al variare di l (tale valore è detto diametro dell’albero).
Per esempio, nel caso riportato in figura il diametro sarà 3:
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 1 | B |
| (12) | B |
| (123) | N |
| (1(23)) | B |
| ((12)(1(23)3)) | N |
Problema 9 – Albero binario
Un albero è binario se e solo se ogni nodo ha al più due figli.
Si scriva il programma di una macchina di Turing che scriva B sul nastro se un albero è binario, N altrimenti.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 1 | B |
| (12) | B |
| (123) | N |
| (1(23)) | B |
| ((12)(1(23)3)) | N |
Problema 10 – Algebra Booleana
L’algebra booleana opera su due soli valori, detti vero e falso, spesso codificati con 1 (per vero) e 0 (per falso).
Su questi valori booleani sono definiti un certo numero di operatori, fra cui l’operatore unario not (negazione) e gli operatori binariand (congiunzione), or (disgiunzione), imp (implicazione) e eqv (equivalenza).
Il valore calcolato da questi operatori è definito dalle seguenti tabelle di verità: ???
Una espressione booleana è costituita da una sequenza di valori booleani e relativi operatori, con l’aggiunta di parentesi per indicare l’ordine di valutazione (le espressioni più interne vanno valutate per prime).
Si scriva un programma che, ricevuta in ingresso una espressione booleana, lasci sul nastro il risultato della sua valutazione (che sarà, ovviamente, uno dei due valori possibili: 0 o 1).
Si assuma che
- l’operatore not sia codificato con il simbolo “!”
- l’and con “*”
- l’or con “+”
- l’imp con “-”
- l’eqv con “=”.
| NASTRO INIZIALE | NASTRO FINALE |
|---|---|
| 0=0 | 1 |
| 1+(0=0) | 1 |
| 1*(1-0) | 0 |
| 1 | 1 |
| (0+(0-(1=0)))+(!0) | 0 |