Numeri di Fibonacci

di

I numeri di Fibonacci prendono il nome da una sfida matematica che Fibonacci lanciò a un suo collega.
Il problema tratta la proverbiale velocità con cui i conigli si riproducono:

  • il 1° mese è presente una coppia di conigli
  • una coppia di conigli diventa matura all’inizio del 2° mese di vita
  • la gestazione dura un mese
  • ogni parto produce una coppia maschio-femmina di conigli
  • ogni coppia di conigli sopravvive e si riproduce per sempre…

Calcolare il numero di coppie di conigli dopo 10 mesi.

Analisi

Tramite i pulsanti puoi osservare l’evoluzione della popolazione di conigli fino al sesto mese

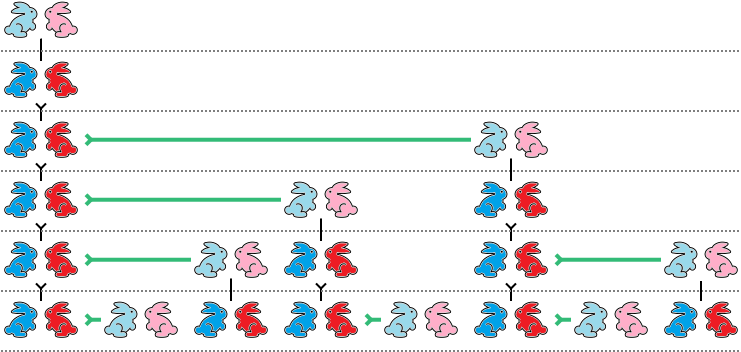
Ogni mese sono presenti i conigli già presenti il mese precedente più quelli appena nati, che sono in numero uguale ai conigli presenti due mesi prima!

I numeri di Fibonacci sono proprio la successione 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … cioè il numero di coppie di conigli per ogni mese.

Al decimo mese ci saranno 55 coppie di conigli.

Algoritmo iterativo

A partire dai valori noti (1, 1) si calcola, mese dopo mese, un nuovo valore finché non si giunge al mese richiesto.

Per calcolare fibonacci(5) si seguono i passi

fibonacci(1) = 1
fibonacci(2) = 1
fibonacci(3) = fibonacci(2)+fibonacci(1) = 1+1 = 2
fibonacci(4) = fibonacci(3)+fibonacci(2) = 2+1 = 3
fibonacci(5) = fibonacci(4)+fibonacci(3) = 3+2 = 5
Function fibonacci(n: Integer): LongInt;
Var
   i      : Integer;
   a, b, c: LongInt;
Begin
   If(n <= 2) Then
      fibonacci:=1
   Else
      Begin
         a:=1;
         b:=1;
         For i:=3 To n Do
            Begin
               c:=a+b;
               a:=b;
               b:=c;
            End;
         fibonacci:=c;
      End;
End;

Algoritmo ricorsivo

La formulazione ricorsiva dei numeri di Fibonacci è molto comoda perché sintetica

image

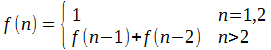
Per calcolare fibonacci(5) si seguono i passi

fibonacci(5) = fibonacci(4)+fibonacci(3)
= (fibonacci(3)+fibonacci(2)) + (fibonacci(2)+fibonacci(1))
= ((fibonacci(2)+fibonacci(1)) + 1) + (1+1)
= ((1+1)+1)+(1+1)
= 5
Function fibonacci(n: Integer): LongInt;
Begin
   If(n <= 2) Then
      fibonacci:=1
   Else
      fibonacci:=fibonacci(n-1)+fibonacci(n-2);
End;

Con formula!

Non è necessario alcun algoritmo iterativo o ricorsivo se si utilizza la formula

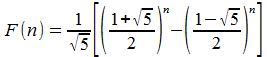
fibonacci2

Il contributo del secondo termine è così piccolo che può essere trascurato. Calcola il primo termine e considera l'intero più vicino (arrotonda).

Dopo aver analizzato il problema e individuati i 3 algoritmi discutiamo la loro complessità in tempo.

Algoritmo ricorsivo

Il tempo di attesa può essere considerato proporzionale al numero di chiamate ricorsive

T(1) = 1
T(2) = 1
T(3) = 1+T(2)+T(1) = 1+1+1 = 3 > 22-1
T(4) = 1+T(3)+T(2) = 1+3+1 = 5 > 22-1
T(5) = 1+T(4)+T(3) = 1+5+3 = 9 > 23-1
T(6) = 1+T(5)+T(4) = 1+9+5 = 15 > 23-1
T(7) = 1+T(6)+T(5) = 1+15+9 = 25 > 24-1
T(8) = 1+T(7)+T(6) = 1+25+15 = 41 > 24-1
...
T(n) ≥ 2n/2-1.

Il tempo di attesa è maggiore di un tempo esponenziale, anche se con esponente n/2 piuttosto che n, quindi per n molto grande

T(n) ∈ O(2n).

L'algoritmo ricorsivo per il calcolo dell'n-simo numero di Fibonacci ha complessità esponenziale!

Algoritmo iterativo

Si tratta di un algoritmo con un'iterazione semplice, senza chiamate ricorsive, quindi

T(n)=c1+c2n
T(n) ∈ O(n).

L'algoritmo iterativo per il calcolo dell'n-simo numero di Fibonacci ha complessità lineare!

Con formula

Se consideriamo costante il tempo necessario per svolgere le singole operazioni presenti nella formula allora

T(n)=c
T(n) ∈ O(1).

Se consideriamo che per n molto grande l'operazione di elevamento a potenza potrebbe dipendere dal numero di cifre e che il numero di cifre del risultato cresce proporzionalmente a n allora si ottiene di nuovo una complessità lineare.

Conclusioni

Dato un certo problema, il calcolo dell'n-esimo numero di Fibonacci, possiamo individuare diversi algoritmi con complessità diverse.
Al variare di n utilizzeremo l'algoritmo più conveniente!