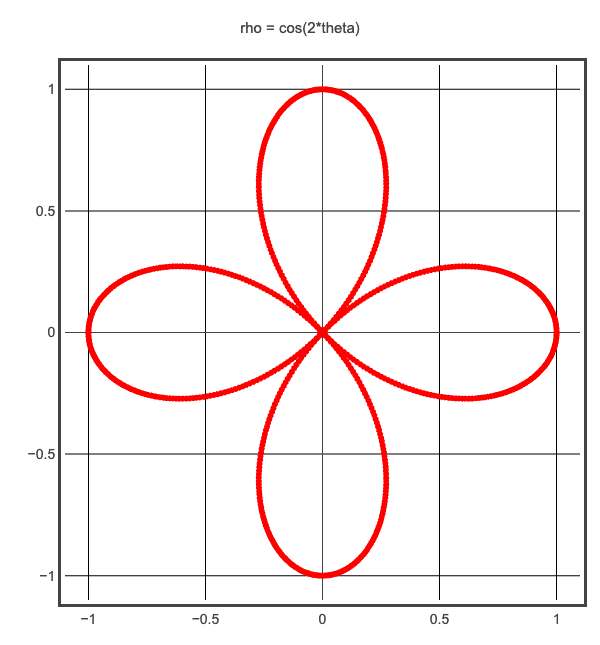
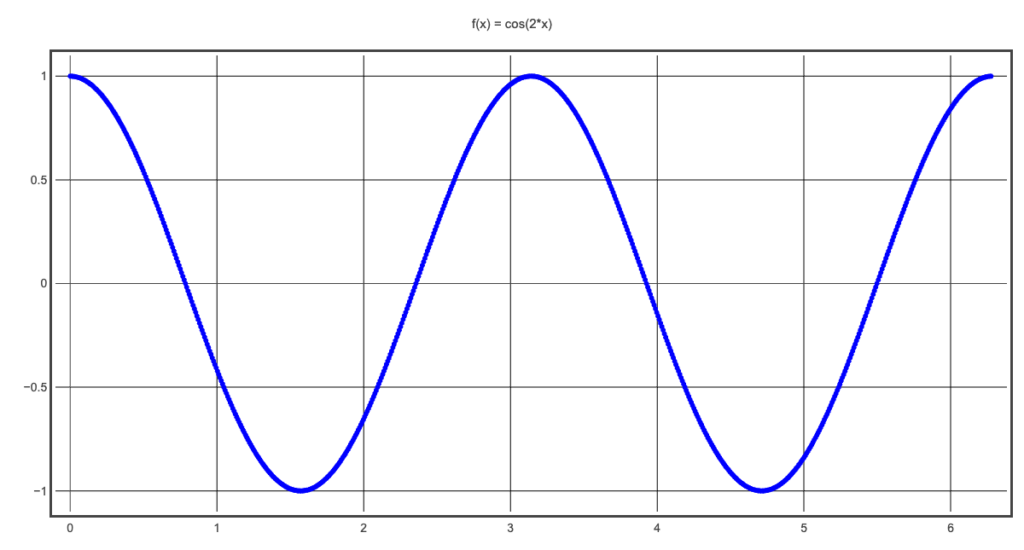
L’animazione del disegno in coordinate polari accompagnata dall’andamento della stessa funzione in coordinate cartesiane.
Lo stesso progetto può essere applicato a tutti i grafici in coordinate polari.
from vpython import *
############################################
def funzione(x): return cos(2*x)
############################################
DIMENSIONE = 600 # ALTEZZA GRAFICI
DURATA = 6 # Durata animazione
NUMERO = 720 # Numero punti calcolati
RATE = NUMERO/DURATA # Frame al secondo
W1 = H1 = H2 = DIMENSIONE
W2 = 2*W1
STOP = 2*pi # Ultimo valore angolo
DELTA = STOP/NUMERO # Variazione angolo
DIM = 1.1 # Valore massimo assi
g1 = graph(align="left" , fast=False, title="rho = cos(2*theta)",
width=W1, height=H1, xmin=-DIM, xmax=DIM , ymin=-DIM, ymax=DIM)
g2 = graph(align="right", fast=False, title="f(x) = cos(2*x)" ,
width=W2, height=H2, xmin=-.1 , xmax=STOP+.1, ymin=-DIM, ymax=DIM)
gd1 = gdots(graph=g1, color=color.red )
gd2 = gdots(graph=g2, color=color.blue)
angolo = 0 # theta
for i in range(NUMERO):
rate(RATE)
r = funzione(angolo) # rho, distanza dal centro
x = r*cos(angolo)
y = r*sin(angolo)
gd1.plot(pos=(x,y))
gd2.plot(pos=(angolo,r))
angolo += DELTA