La legge di Hooke – 1

di

Un oggetto si muove in orizzontale secondo la legge di Hooke

\vec{F} = -k\cdot \vec{x}
\displaystyle \vec{F} = m \vec{a}\displaystyle \vec{a} = \frac{\vec{F}}{m}
\vec{v_0} = \vec{0}\displaystyle \frac{\vec{\Delta v}}{\Delta t} = \vec{a}\displaystyle \vec{\Delta v} = \vec{a}\cdot \Delta t\vec{v}\ \ +=\ \ \vec{\Delta v}
\vec{s_0} = \dots\displaystyle \frac{\vec{\Delta s}}{\Delta t} = \vec{v}\displaystyle \vec{\Delta s} = \vec{v}\cdot \Delta t\vec{s}\ \ += \ \ \vec{\Delta s}

La posizione iniziale dipende dalla costante START

from vpython import *

DIM   = 1       # LATO DEL CUBO
START = +DIM    # ASCISSA POSIZIONE INIZIALE
SPESS = DIM/10

parete    = box  (pos=vector(-2*DIM, 0, 0)        , size=vector(SPESS, DIM, DIM))
pavimento = box  (pos=vector(0, -(DIM+SPESS)/2, 0), size=vector(4*DIM, SPESS, DIM))
zero      = box  (pos=vector(0, -(DIM+SPESS)/2, 0), size=vector(SPESS, SPESS, DIM), 
                  color=color.red)
molla     = helix(pos=vector(-2*DIM, 0, 0)        , size=vector(DIM+START, DIM/2, DIM/2), 
                  color=color.cyan  , coils=20)  
oggetto   = box  (pos=vector(START, 0, 0)         , size=vector(DIM, DIM, DIM), 
                  color=color.yellow)

oggetto.velocità = vector(0,0,0)
  
k = 1     # costante elastica
m = 1     # massa dell'oggetto
t = 0     # tempo

dt = 0.05
while(True):
    rate(25)
  
    F = -k*oggetto.pos.x
    a = F/m
      
    oggetto.velocità += vector(a, 0, 0) * dt
    oggetto.pos      += oggetto.velocità * dt  
    molla.length      = 2*DIM + oggetto.pos.x
  
    t += dt

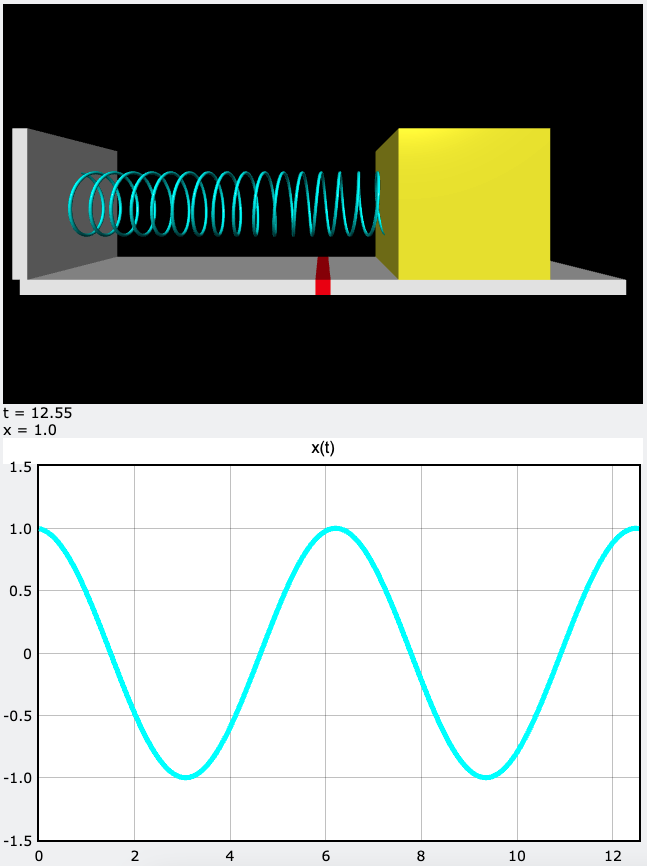
Il grafico rappresenta la posizione dell’oggetto al variare del tempo.

from vpython import *

c  = canvas()
g  = graph(title = "x(t)")
gc = gcurve(color=color.cyan, width=5)


DIM   = 1       # LATO DEL CUBO
START = +DIM    # ASCISSA POSIZIONE INIZIALE
SPESS = DIM/10

parete    = box  (pos=vector(-2*DIM, 0, 0)        , size=vector(SPESS, DIM, DIM))
pavimento = box  (pos=vector(0, -(DIM+SPESS)/2, 0), size=vector(4*DIM, SPESS, DIM))
zero      = box  (pos=vector(0, -(DIM+SPESS)/2, 0), size=vector(SPESS, SPESS, DIM)      , 
                  color=color.red)
molla     = helix(pos=vector(-2*DIM, 0, 0)        , size=vector(DIM+START, DIM/2, DIM/2), 
                  color=color.cyan  , coils=20)  
oggetto   = box  (pos=vector(START, 0, 0)         , size=vector(DIM, DIM, DIM)          , 
                  color=color.yellow)

oggetto.velocità = vector(0,0,0)
  
k = 1     # costante elastica
m = 1     # massa dell'oggetto
t = 0     # tempo

dt = 0.05
while(t < 2*tau):
    rate(25)
  
    F = -k*oggetto.pos.x
    a = F/m
      
    oggetto.velocità += vector(a, 0, 0) * dt
    oggetto.pos      += oggetto.velocità * dt  
    molla.length      = 2*DIM + oggetto.pos.x

    gc.plot(t, oggetto.pos.x)
    c.caption = "t = "   + str(round(t, 2))             + \
                "\nx = " + str(round(oggetto.pos.x, 2))
  
    t += dt

Lascia un commento