La circonferenza al centro è costituita da NCIRCO punti distinti.
La circonferenza in movimento ha il centro in un punto della circonferenza centrale ed è costituita da Ncirco tratti continui.
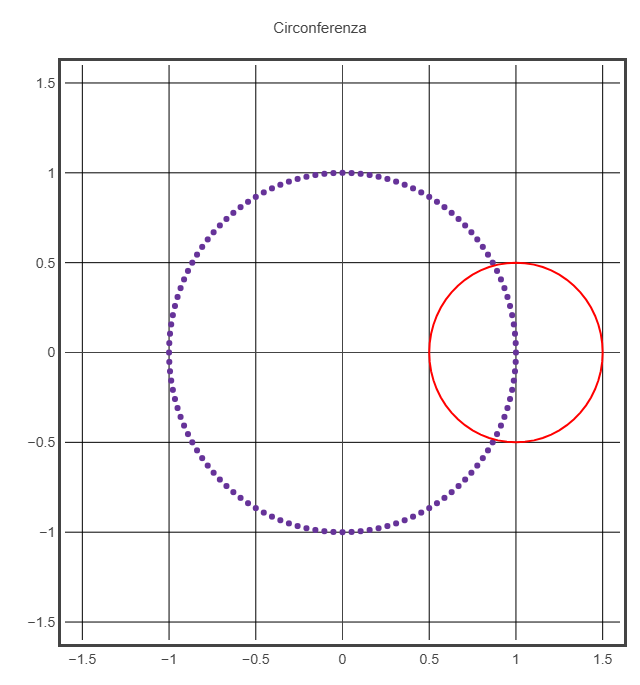
Le immagini successive sono inviluppi di circonferenze intorno alla circonferenza centrale.
L’animazione ha una durata prefissata.
Ciambella (toro)
Il raggio esterno è costante
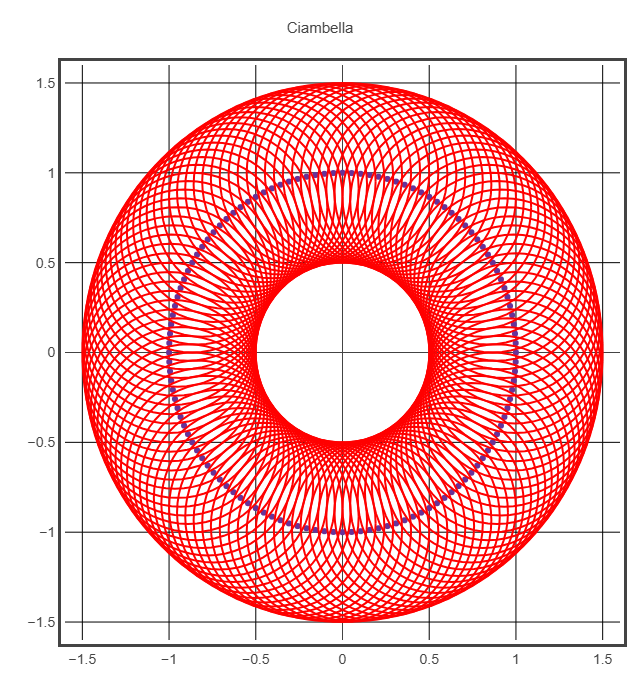
from vpython import *
R = 1.0 # Raggio centrale
r = 0.5 # Raggio esterno
DIM = R+r+0.1 # Distanza massima finestra
Ncirco = 60 # Numero tratti
NCIRCO = 120 # Numero punti
DURATA = 6 # Durata dell'animazione
RATE = NCIRCO/DURATA # Numero cerchi al secondo
STOP = tau # Angolo percorso
DELTA_a = STOP/Ncirco # Passo angolo esterno
DELTA_A = STOP/NCIRCO # Passo angolo centrale
def circonferenza(xc, yc):
gc = gcurve(color=color.red)
angolo = 0
for i in range(Ncirco+1):
x = xc+r*cos(angolo)
y = yc+r*sin(angolo)
gc.plot(pos=(x,y))
angolo += DELTA_a
graph(title="Ciambella",
width=640, height=640, xmin=-DIM, ymin=-DIM, xmax=DIM, ymax=DIM,
fast=False)
gf=gdots(color=color.purple)
ANGOLO = 0
for i in range(NCIRCO):
rate(RATE)
x = R*cos(ANGOLO)
y = R*sin(ANGOLO)
gf.plot(pos=(x,y))
circonferenza(x,y)
ANGOLO += DELTA_A
Per realizzare le figure successive bisogna stabilire la funzione per la dimensione variabile del raggio esterno.
Nefroide
r = abs(xc), il raggio esterno è dato dalla distanza dall’asse yDIM = R+R+0.1
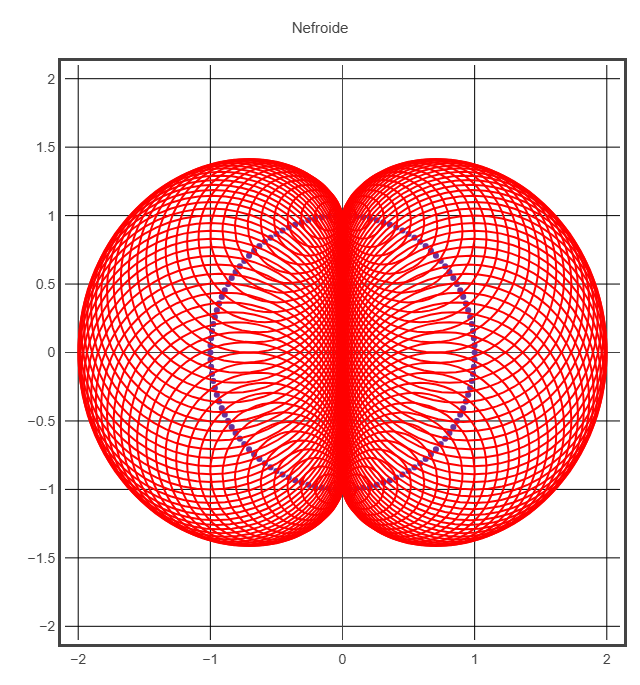
from vpython import *
R = 1.0
DIM = R+R+0.1 # <---
Ncirco = 60
NCIRCO = 120
DURATA = 6
RATE = NCIRCO/DURATA
STOP = tau
DELTA_a = STOP/Ncirco
DELTA_A = STOP/NCIRCO
def circonferenza(xc, yc):
gc = gcurve(color=color.red)
angolo = 0
for i in range(Ncirco+1):
r = abs(xc) # <---
x = xc+r*cos(angolo)
y = yc+r*sin(angolo)
gc.plot(pos=(x,y))
angolo += DELTA_a
graph(title="Nefroide",
width=640, height=640, xmin=-DIM, ymin=-DIM, xmax=DIM, ymax=DIM,
fast=False)
gf=gdots(color=color.purple)
ANGOLO = 0
for i in range(NCIRCO):
rate(RATE)
x = R*cos(ANGOLO)
y = R*sin(ANGOLO)
gf.plot(pos=(x,y))
circonferenza(x,y)
ANGOLO += DELTA_A
Cardioide
r = dist((xc, yc), (0, 1)), il raggio esterno è dato dalla distanza dalla cuspideDIM = R+R+R+0.1
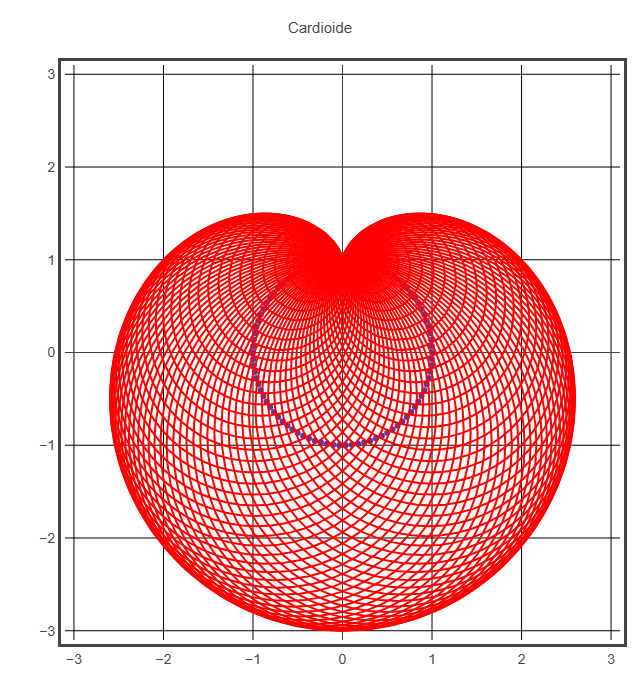
Lumaca di Pascal
r = dist((xc, yc), (0, 1)) / 2, il raggio esterno è dato dalla metà della distanza dalla cuspideDIM = R+R+0.1
