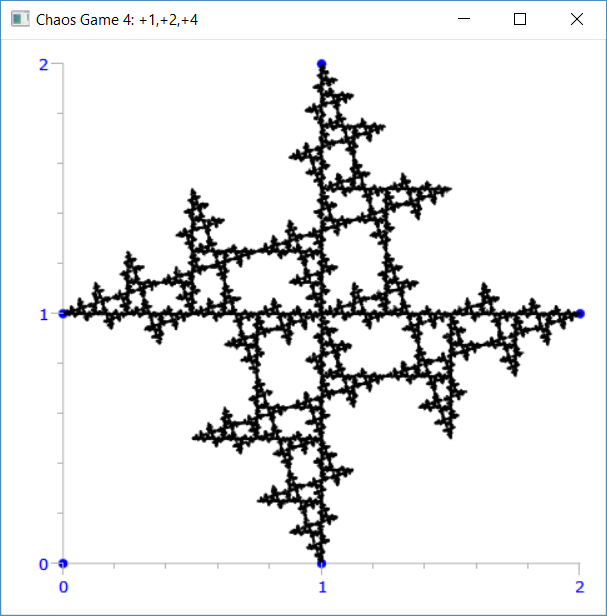
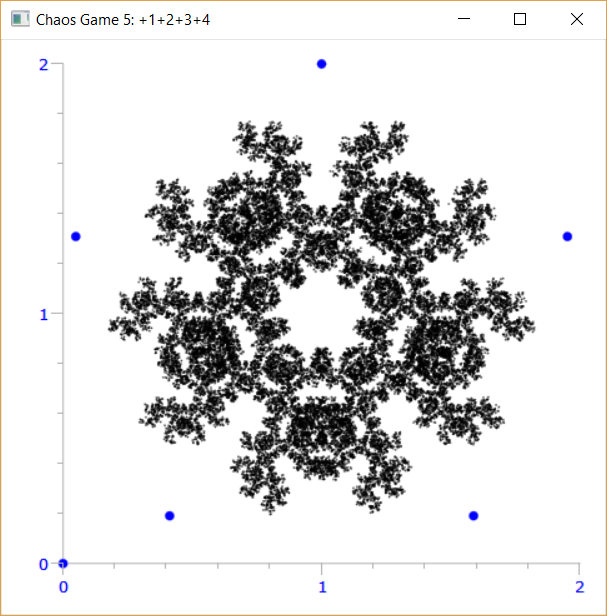
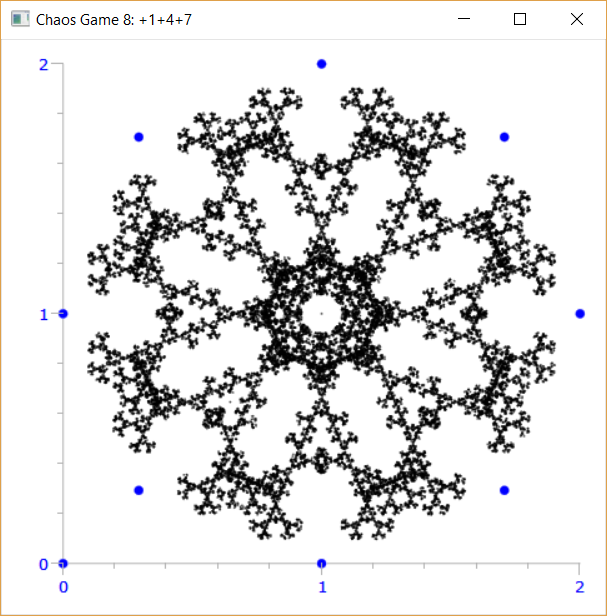
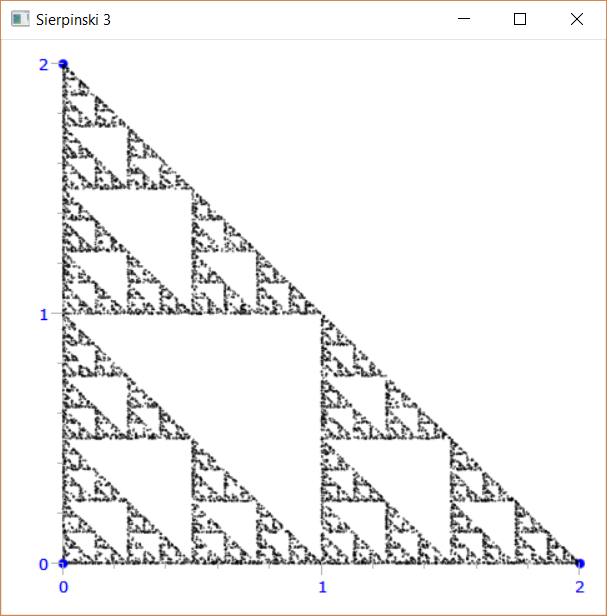
I frattali seguenti sono realizzati tramite delle regole molto elementari
- un certo numero di punti fissi, vertici
- un punto che salta da un vertice all’altro in modo casuale
from visual import *
from visual.graph import *
from random import *
NVERTICI=3
DURATA =5
NPUNTI =10000
RATE =NPUNTI/DURATA
DIM=2
O=vector(0 , 0)
A=vector(DIM, 0)
B=vector(0 ,DIM)
VERTICI=(O,A,B)
gdisplay(title="Sierpinski 3",
xmin=0,xmax=DIM, ymin=0,ymax=DIM, width=500,height=500,
background=color.white, foreground=color.blue)
g=gdots(size=8, color=color.blue)
for p in VERTICI:
g.plot(pos=p)
g=gdots(size=1, color=color.black)
p=VERTICI[0]
for i in range(NPUNTI):
rate(RATE)
pos=randint(0,NVERTICI-1)
p=(p+VERTICI[pos])/2
g.plot(pos=p)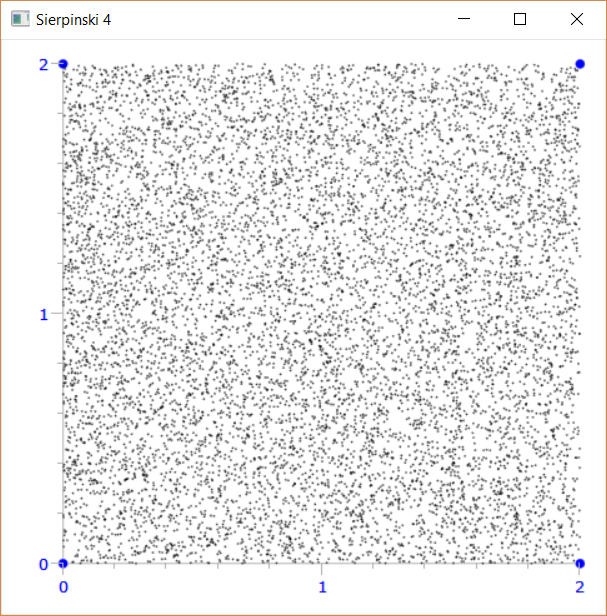
Con 4 vertici si ottiene il caos
Ritorna la regolarità con la nuova regola per la posizione del punto
- p=(p+2*VERTICI[pos])/3
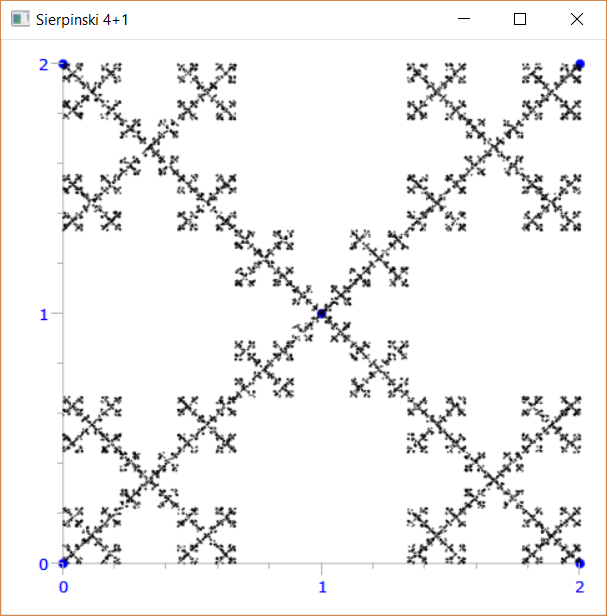
Si ottiene un frattale molto noto aggiungendo un punto al centro
from visual import *
from visual.graph import *
from random import *
NVERTICI=5
DURATA =5
NPUNTI =10000
RATE =NPUNTI/DURATA
DIM=2
O=vector(0 ,0 )
A=vector(DIM ,0 )
B=vector(DIM ,DIM )
C=vector(0 ,DIM )
D=vector(DIM/2,DIM/2)
VERTICI=(O,A,B,C,D)
gdisplay(title="Sierpinski 4+1",
xmin=0,xmax=DIM, ymin=0,ymax=DIM, width=500,height=500,
background=color.white,foreground=color.blue)
g=gdots(size=8, color=color.blue)
for p in VERTICI:
g.plot(pos=p)
g=gdots(size=1, color=color.black)
p=VERTICI[0]
for i in range(NPUNTI):
rate(RATE)
pos=randint(0,NVERTICI-1)
p=(p+2*VERTICI[pos])/3
g.plot(pos=p)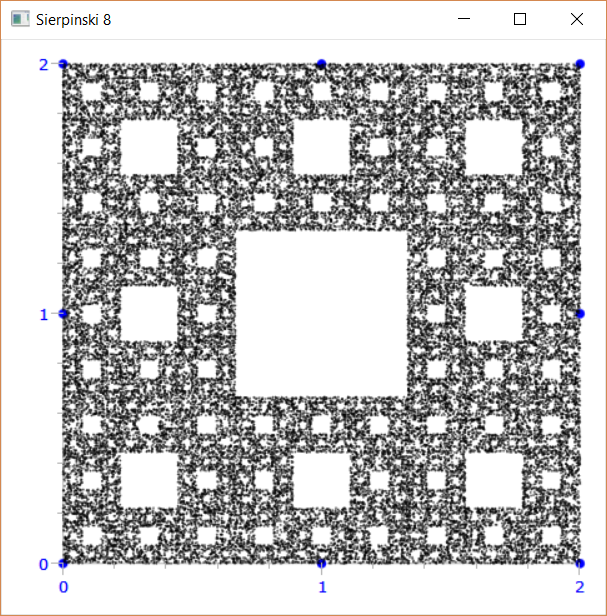
Un altro frattale molto noto con 8 vertici
from visual import *
from visual.graph import *
from random import *
NVERTICI=8
NPUNTI =50000
DURATA =5
RATE =NPUNTI/DURATA
DIM=2
O=vector(0 ,0 )
A=vector(DIM/2,0 )
B=vector(DIM ,0 )
C=vector(DIM ,DIM/2)
D=vector(DIM ,DIM )
E=vector(DIM/2,DIM )
F=vector(0 ,DIM )
G=vector(0 ,DIM/2)
VERTICI=(O,A,B,C,D,E,F,G)
gdisplay(title="Sierpinski 8",
xmin=0,xmax=DIM, ymin=0,ymax=DIM, width=500,height=500,
background=color.white,foreground=color.blue)
g=gdots(size=8, color=color.blue)
for p in VERTICI:
g.plot(pos=p)
g=gdots(size=1, color=color.black)
p=VERTICI[0]
for i in range(NPUNTI):
rate(RATE)
pos=randint(0,NVERTICI-1)
p=(p+2*VERTICI[pos])/3
g.plot(pos=p)
Il prossimo punto può dirigersi solo verso alcuni vertici
- +1, +4, +7
from visual import *
from visual.graph import *
from random import *
CHOICE =[+1,+4,+7]
NVERTICI=8
NPUNTI =50000
DURATA =5
RATE =NPUNTI/DURATA
DIM =2
LVERTICI=NVERTICI*[vector(0,0)]
LVERTICI[0]=vector(0 , 0 )
LVERTICI[1]=vector(DIM/2, 0 )
LVERTICI[2]=vector(DIM , 0 )
LVERTICI[3]=vector(DIM , DIM/2)
LVERTICI[4]=vector(DIM , DIM )
LVERTICI[5]=vector(DIM/2, DIM )
LVERTICI[6]=vector(0 , DIM )
LVERTICI[7]=vector(0 , DIM/2)
gdisplay(title="CHAOS GAME: +1+4+7",
xmin=0,xmax=DIM, ymin=0,ymax=DIM, width=500,height=500,
background=color.white,foreground=color.blue)
g=gdots(size=8, color=color.blue)
for i in range(NVERTICI):
g.plot(pos=LVERTICI[i])
g=gdots(size=1, color=color.black)
p=LVERTICI[0]
pos=0
for i in range(NPUNTI):
rate(RATE)
pos+=choice(CHOICE)
if(pos >= NVERTICI):
pos-=NVERTICI
p=(p+LVERTICI[pos])/2
g.plot(pos=p)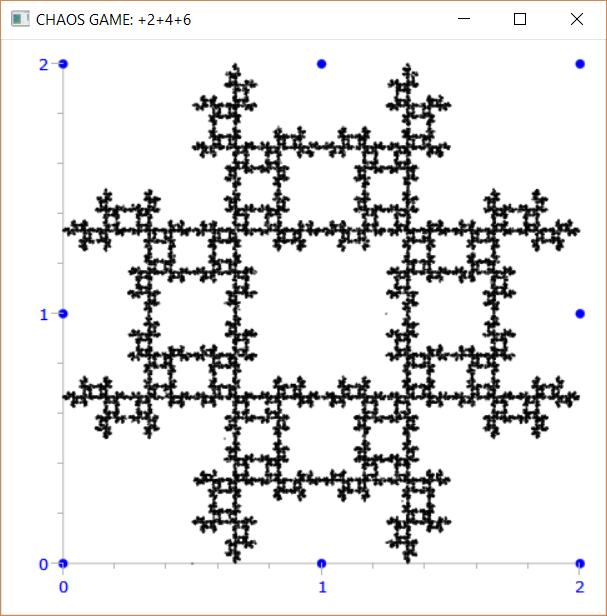
- +2, +4, +6
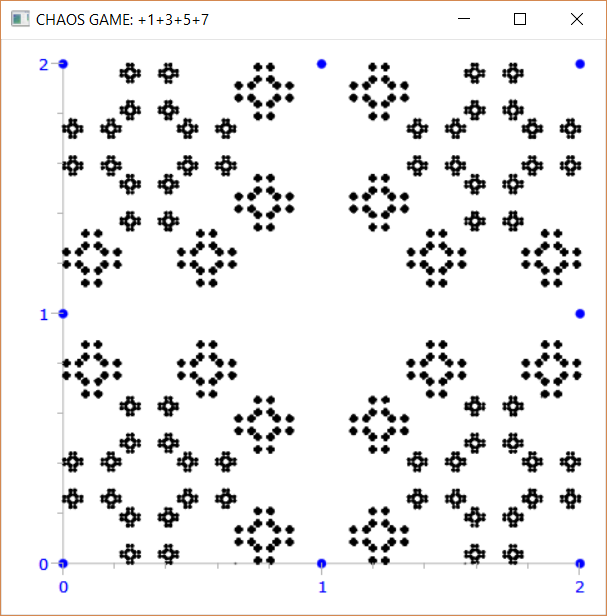
- +1, +3, +5, +7
- p=(p+2*LVERTICI[pos])/3
…Sperimenta cambiando l’elenco delle mosse e la regola…
Si ottiene una nuova famiglia di immagini interessanti ripetendo tutti i passaggi precedenti ma disponendo i vertici in circolo
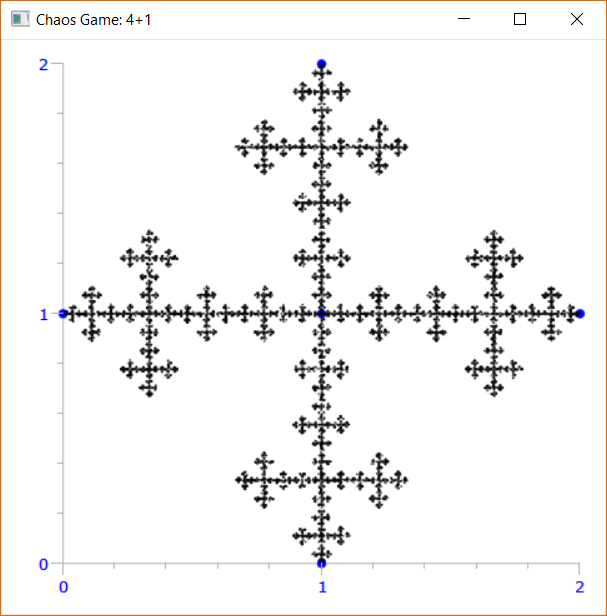
4+1
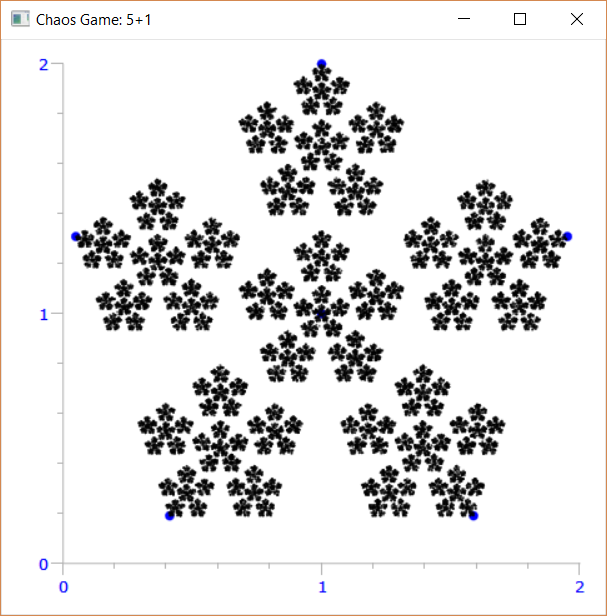
5+1
from visual import *
from visual.graph import *
from random import *
NVERTICI=5
NPUNTI =40000
DURATA =5
RATE =NPUNTI/DURATA
VERTICI=(NVERTICI+1)*[vector(0,0)]
DIM=2
gdisplay(title="Chaos Game: 5+1",
xmin=0,xmax=DIM, ymin=0,ymax=DIM, width=500,height=500,
background=color.white,foreground=color.blue)
g=gdots(size=8, color=color.blue)
ALFA=2*pi/NVERTICI
alfa=pi/2
for i in range(0,NVERTICI):
VERTICI[i]=vector(1+cos(alfa),1+sin(alfa))
g.plot(pos=VERTICI[i])
alfa+=ALFA
VERTICI[NVERTICI]=vector(1,1)
g.plot(pos=VERTICI[NVERTICI])
g=gdots(size=1, color=color.black)
p=VERTICI[0]
for i in range(NPUNTI):
rate(RATE)
pos=randint(0,NVERTICI)
p=(p+2*VERTICI[pos])/3
g.plot(pos=p)
6+1
Continua a indagare…