Satelliti – 2 – Programmare con Python+Turtle

Le funzioni forward() e backward() realizzano la “grafica della tartaruga” calcolando la posizione successiva corrispondente.
Possono essere sostituite con setposition(x, y) e le funzioni seno e coseno!

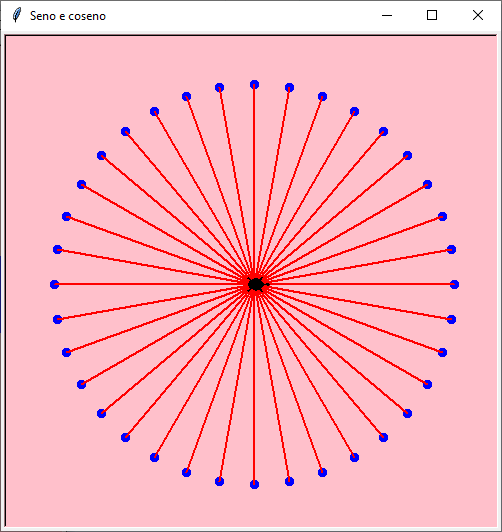
import math    # cos(), radians(), sin()
import turtle  # ...

WIDTH    = 500
HEIGHT   = 500
NUMERO   = 36
COLORE   = 'blue'

DIAMETRO = 10
DELTA    = 360/NUMERO
RAGGIO   = 0.40*WIDTH

turtle.setup(WIDTH, HEIGHT)
turtle.bgcolor('pink')
turtle.pencolor('red')
turtle.pensize(2)
turtle.shape('turtle')
turtle.speed(0)
turtle.title('Seno e coseno')

angolo = 0
for i in range(NUMERO):
    radianti = math.radians(angolo)
    x        = RAGGIO*math.cos(radianti)
    y        = RAGGIO*math.sin(radianti)
    
    turtle.setposition(x, y)
    turtle.dot(DIAMETRO, COLORE)
    turtle.setposition(0, 0)

    angolo = angolo+DELTA

Non è necessario ritornare ogni volta al centro…

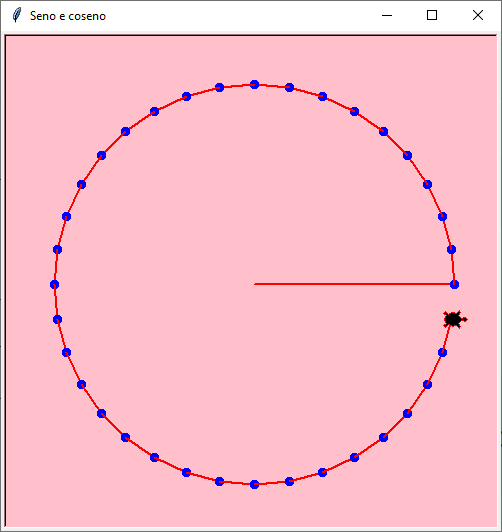
import math    # cos(), radians(), sin()
import turtle  # ...

WIDTH    = 500
HEIGHT   = 500
NUMERO   = 36
COLORE   = 'blue'

DIAMETRO = 10
DELTA    = 360/NUMERO
RAGGIO   = 0.40*WIDTH

turtle.setup(WIDTH, HEIGHT)
turtle.bgcolor('pink')
turtle.pencolor('red')
turtle.pensize(2)
turtle.shape('turtle')
turtle.speed(0)
turtle.title('Seno e coseno')

angolo = 0
for i in range(NUMERO):
    radianti = math.radians(angolo)
    x        = RAGGIO*math.cos(radianti)
    y        = RAGGIO*math.sin(radianti)    

    turtle.setposition(x, y)
    turtle.dot(DIAMETRO, COLORE)

    angolo = angolo+DELTA

Anche il primo raggio può essere nascosto e il percorso può essere chiuso!

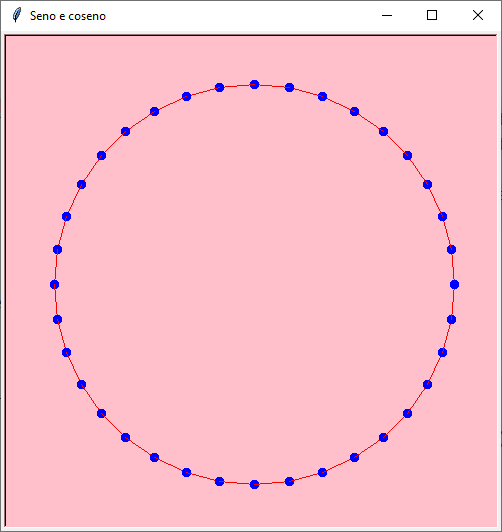
import math    # cos(), radians(), sin()
import turtle  # ...

WIDTH    = 500
HEIGHT   = 500
NUMERO   = 36
COLORE   = 'blue'

DIAMETRO = 10
DELTA    = 360/NUMERO
RAGGIO   = 0.40*WIDTH

turtle.setup(WIDTH, HEIGHT)
turtle.bgcolor('pink')
turtle.hideturtle()
turtle.pencolor('red')
turtle.speed(0)
turtle.title('Seno e coseno')

angolo   = 0
radianti = math.radians(angolo)
x        = RAGGIO*math.cos(radianti)
y        = RAGGIO*math.sin(radianti)

turtle.penup()
turtle.setposition(x, y)
turtle.pendown()
turtle.dot(DIAMETRO, COLORE)

angolo   = angolo+DELTA
for i in range(NUMERO):
    radianti = math.radians(angolo)
    x        = RAGGIO*math.cos(radianti)
    y        = RAGGIO*math.sin(radianti)    
    turtle.setposition(x, y)
    turtle.dot(DIAMETRO, COLORE)
    angolo   = angolo+DELTA

Si può disegnare facilmente un poligono regolare con numero di lati a piacere

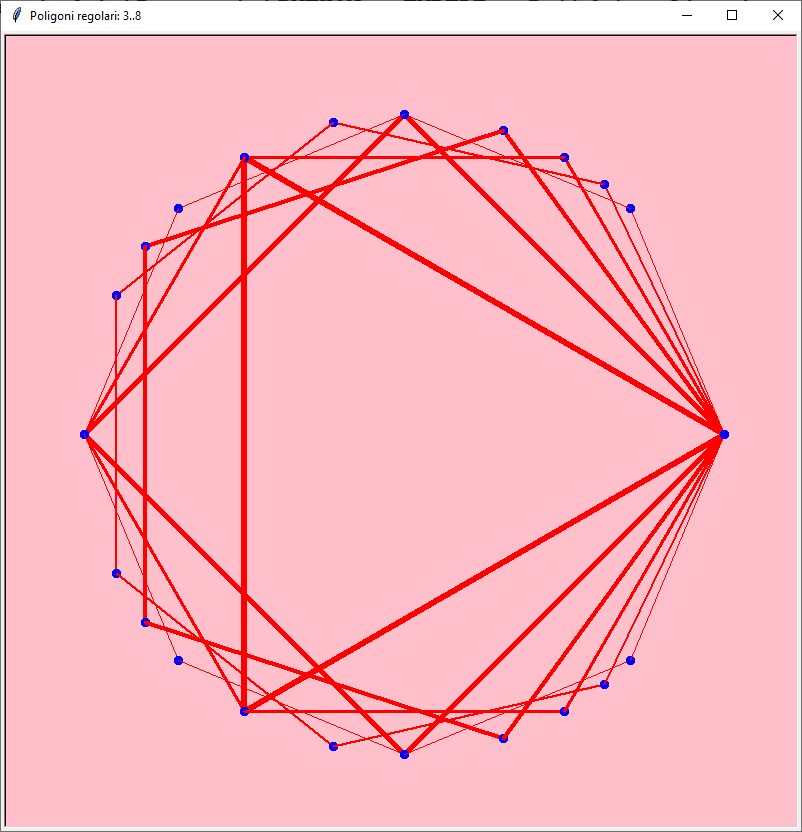
import math    # cos(), radians(), sin()
import turtle  # ...

WIDTH    = 800
HEIGHT   = 800
COLORE   = 'blue'
ULTIMO   = 8

DIAMETRO = 10
RAGGIO   = 0.40*WIDTH

turtle.setup(WIDTH, HEIGHT)
turtle.bgcolor('pink')
turtle.hideturtle()
turtle.pencolor('red')
turtle.speed(0)
turtle.title('Poligoni regolari: 3..' + str(ULTIMO))

for numero in range(3, ULTIMO+1):
    DELTA    = 360/numero
    angolo   = 0
    radianti = math.radians(angolo)
    x        = RAGGIO*math.cos(radianti)
    y        = RAGGIO*math.sin(radianti)

    turtle.pensize(ULTIMO+1-numero)
    turtle.penup()
    turtle.setposition(x, y)
    turtle.pendown()
    turtle.dot(DIAMETRO, COLORE)

    angolo   = angolo+DELTA
    for i in range(numero):
        radianti = math.radians(angolo)
        x        = RAGGIO*math.cos(radianti)
        y        = RAGGIO*math.sin(radianti)    

        turtle.setposition(x, y)
        turtle.dot(DIAMETRO, COLORE)

        angolo   = angolo+DELTA

Lascia un commento Annulla risposta