La forma iniziale assomiglia alla punta seghettata di una freccia ma al limite si ottiene il triangolo di Sierpinski!
Ricorsione da 1 a 7
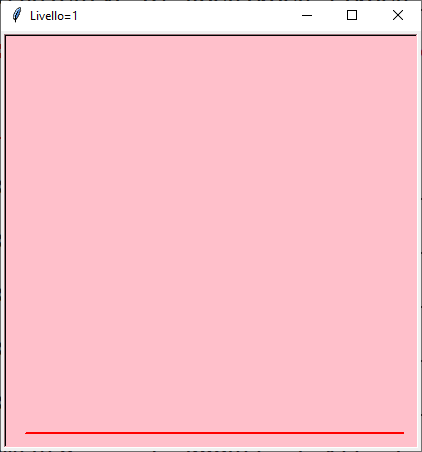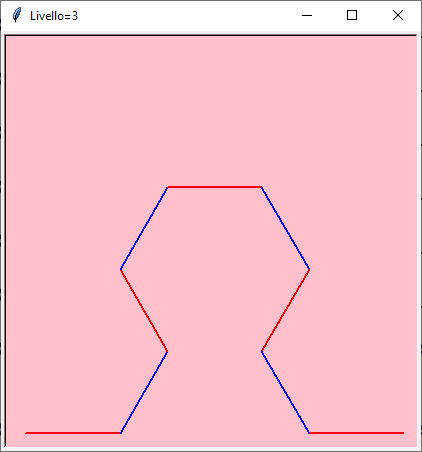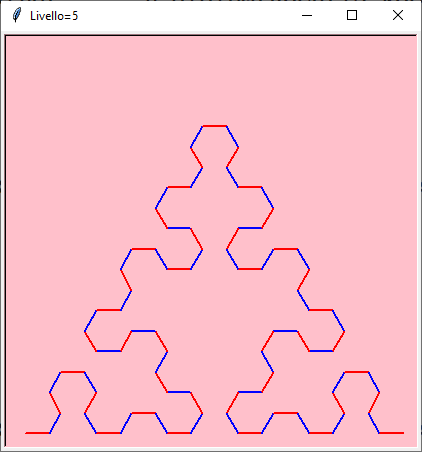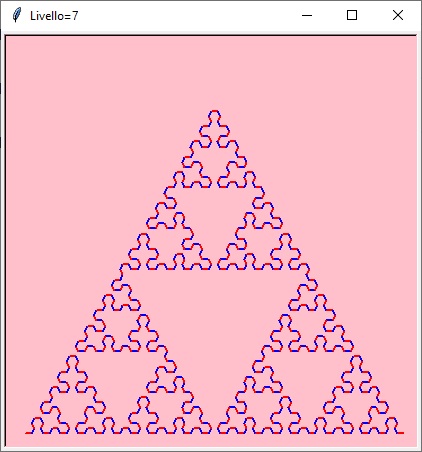
Scarica le immagini singole: arrowhead-1 — arrowhead-2 — arrowhead-3 — arrowhead-4 — arrowhead-5 — arrowhead-6 — arrowhead-7
Ricorsione=8
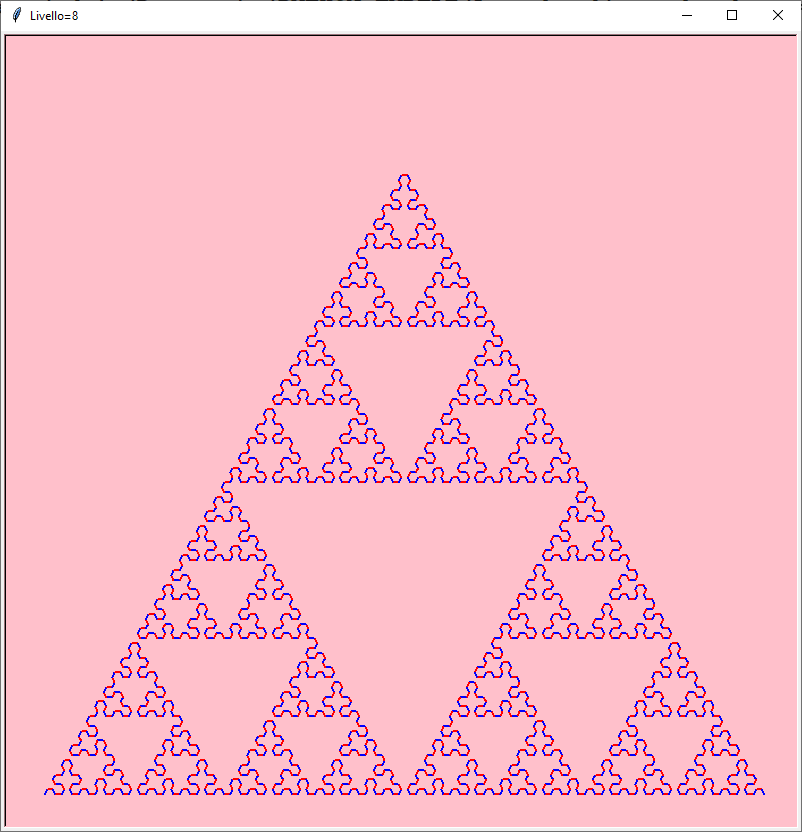
Ricorsione=9

import turtle # ...
import math # sqrt()
import time # sleep()
def set_all():
global POSIZIONE, DISTANZA, DISTANZE, RIC_MAX, POS_X, POS_Y
WIDTH = 800 # larghezza finestra
HEIGHT = 800 # altezza finestra
RIC_MAX = 9 # massima ricorsione
POS_X = -WIDTH*0.45 # posizione iniziale
POS_Y = -HEIGHT*0.45 # posizione iniziale
DISTANZA = WIDTH*0.9
DISTANZE = [0]*(RIC_MAX+1) # dimensioni successive
turtle.setup(width=WIDTH, height=HEIGHT)
turtle.hideturtle()
turtle.bgcolor("pink")
turtle.tracer(0)
def start_draw(r):
DISTANZE[r] = DISTANZA
for i in range(r-1,0,-1):
DISTANZE[i]=DISTANZE[i+1]/2
turtle.penup()
turtle.setposition(POS_X, POS_Y)
turtle.setheading(0)
turtle.pensize(RIC_MAX-r+2)
turtle.pendown()
turtle.clear()
turtle.title("Livello="+str(r))
def end_draw():
turtle.update()
time.sleep(2)
def arrowhead1(n):
if(n == 1):
turtle.pencolor('red')
turtle.forward(DISTANZE[n])
else:
turtle.left(60) ; arrowhead2(n-1)
turtle.right(60); arrowhead1(n-1)
turtle.right(60); arrowhead2(n-1)
turtle.left(60)
def arrowhead2(n):
if(n == 1):
turtle.pencolor('blue')
turtle.forward(DISTANZE[n])
else:
turtle.right(60); arrowhead1(n-1)
turtle.left(60) ; arrowhead2(n-1)
turtle.left(60) ; arrowhead1(n-1)
turtle.right(60)
set_all()
for r in range(1,RIC_MAX+1):
start_draw(r)
arrowhead1(r)
end_draw()
turtle.done()
Osserva
- ci sono 2 funzioni mutuamente ricorsive
- disegna le figure successive con pause di 2 secondi
- lo spessore della penna diminuisce all’aumentare della ricorsione
- le distanze da percorrere sono calcolate in anticipo