L-System > Curva di Koch – 1

Vedi la discussione

---

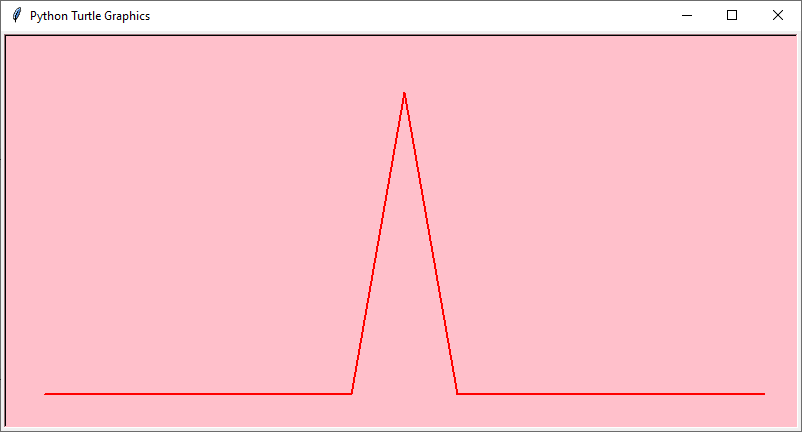
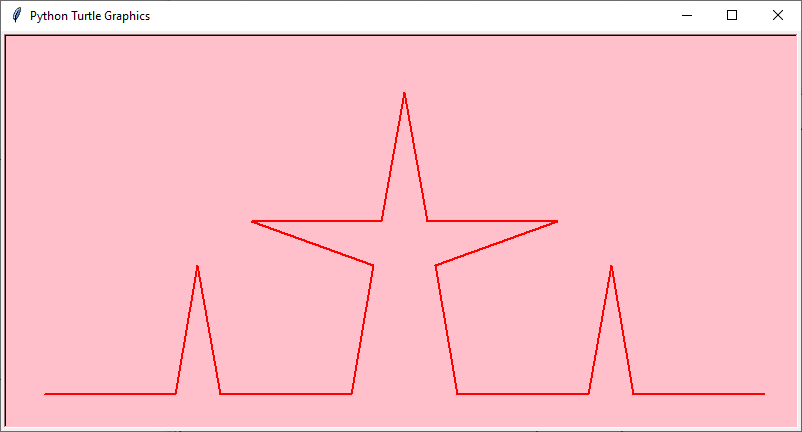
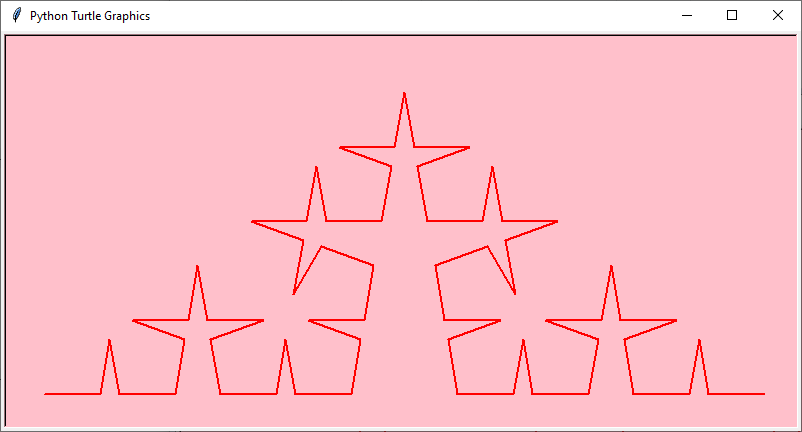
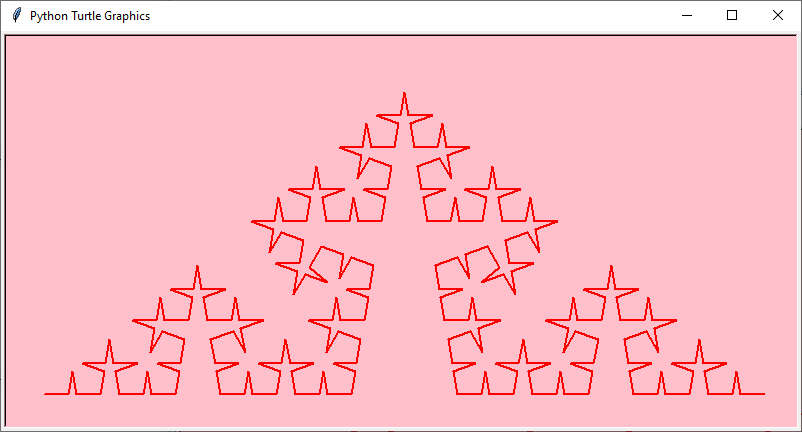
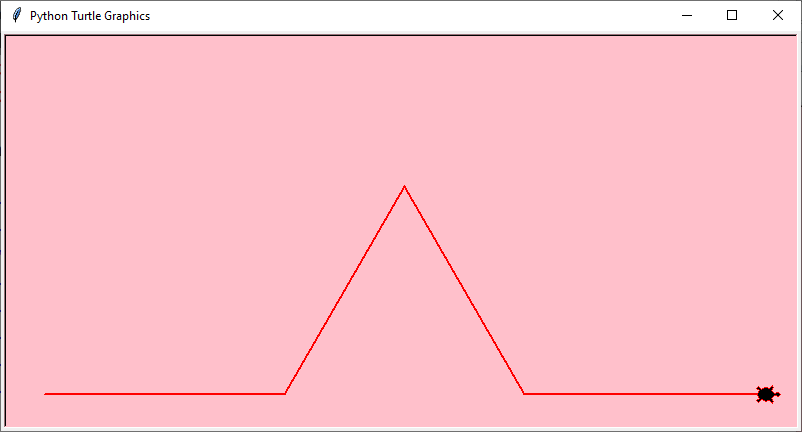
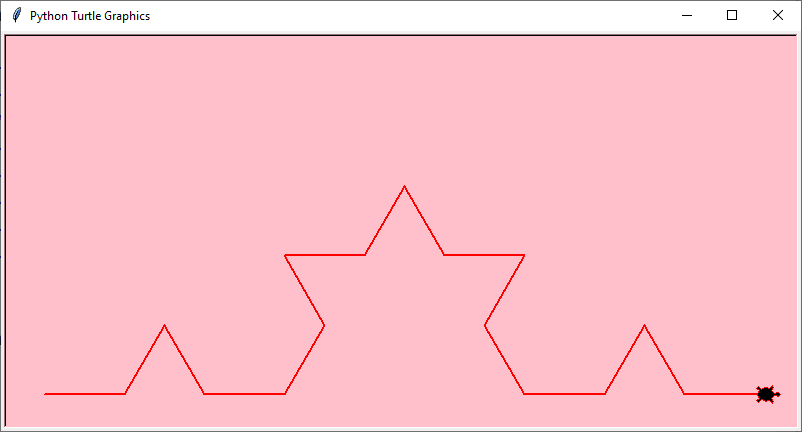
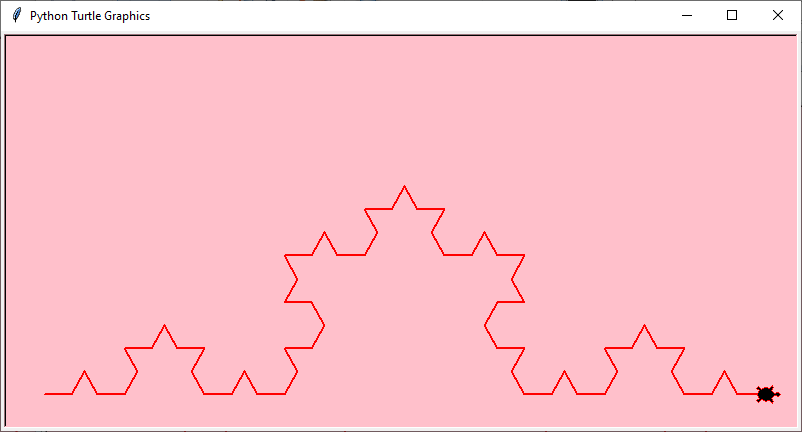
Ecco gli sviluppi al variare del livello di produzione

Codifica

import math
import turtle
#-----------------------------------------------
WIDTH  =800       # Dimensione finestra
HEIGHT =400       # ...
LIVELLI=5         # Numero livelli
#-----------------------------------------------
W      =-WIDTH*0.45      # Posizione iniziale
H      =-HEIGHT*0.4      # ...
DIR    = 0               # Direzione iniziale
ANGOLO = 60              # Angolo a sinistra
#----------------------------------------------- Passo della tartaruga
coseno = math.cos(math.radians(ANGOLO))
SIZE   = WIDTH*0.9 / (2*(1+coseno))**(LIVELLI-1)
#-----------------------------------------------
R      = 'F'
REGOLE = {'F':'F+F--F+F','+':'+', '-':'-'}
#-----------------------------------------------
def trasforma(R):
    R2=''
    for x in R:
        R2 += REGOLE[x]
    return R2
#-----------------------------------------------
def prepara():
    turtle.setup(width=WIDTH, height=HEIGHT)
    turtle.bgcolor('pink')
    turtle.pencolor("red")
    turtle.pensize(2)
    turtle.penup()
    turtle.shape('turtle')
    turtle.speed(0)
    turtle.setposition(W,H)
    turtle.setheading(DIR)
    turtle.pendown()
    #turtle.hideturtle()
#-----------------------------------------------
def disegna(R):    
    STACK=[]
    for x in R:
        if(x == '+'):
            turtle.left(ANGOLO)
        elif(x == '-'):
            turtle.right(ANGOLO)
        elif(x == 'F'):
            turtle.forward(SIZE)
#-----------------------------------------------
for j in range(LIVELLI-1):
    R=trasforma(R)

print(len(R), '\t', str().join(R), '\n')
prepara()
disegna(R)

Se l’angolo è maggiore di 60° (per esempio 80°) si ottengono delle punte più acuminate, al limite si ottiene la curva di Peano 2