Considera una lista di numeri e, per la media pesata, anche una lista di pesi
Media geometrica
![Rendered by QuickLaTeX.com \displaystyle m_g=\sqrt[n]{x_1\cdot x_2 \dots x_n}](https://www.valcon.it/python/wp-content/ql-cache/quicklatex.com-bda1be7457b59d68744a5d6430d2e230_l3.png)
- La radice ennesima del prodotto
NUMERI = [...]
prodotto = 1
for x in NUMERI:
prodotto *= x
n = len(NUMERI)
m_g = prodotto**(1/n)
Da Python 3.8 è disponibile la funzione statistics.geometric_mean(z)
...
m_g = statistics.geometric_mean(NUMERI)
Media quadratica
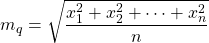
- La radice quadrata della media aritmetica dei quadrati
import math
NUMERI = [...]
somma=0
for x in NUMERI:
somma += x**2
n = len(NUMERI)
m_q = math.sqrt(somma/n)
Media armonica
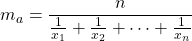
- Il reciproco della media aritmetica dei reciproci
NUMERI = [...]
somma = 0
for x in NUMERI:
somma += 1/x
n = len(NUMERI)
m_a = n/somma
Da Python 3.8 è disponibile la funzione statistics.harmonic_mean(z)
...
m_a = statistics.harmonic_mean(NUMERI)
Media pesata
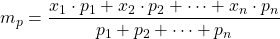
- Il rapporto tra la somma dei prodotti e la somma dei pesi
- La sequenza dei pesi ha la stessa lunghezza della sequenza dei numeri
NUMERI = [...]
PESI = [...]
somma_prod = 0
somma_pesi = 0
n = len(NUMERI)
for i in range(n):
x = NUMERI[i]
p = PESI[i]
somma_prod += x*p
somma_pesi += p
m_p = somma_prod/somma_pesi
Il codice si semplifica utilizzando la funzione zip()
NUMERI = [...]
PESI = [...]
somma_prod = 0
somma_pesi = 0
for x, p in zip(NUMERI, PESI):
somma_prod += x*p
somma_pesi += p
m_p = somma_prod/somma_pesi