1
Due melanzane hanno esattamente lo stesso peso di tre peperoni.
Una melanzana e un peperone pesano insieme 300 grammi.
Sappiamo inoltre che tre melanzane pesano esattamente quanto una barbabietola e un peperone.
Dire quanti grammi pesano rispettivamente una melanzana, un peperone e una barbabietola.
2
Se si lanciano due dadi, qual è la probabilità di fare 6 (naturalmente sommando i valori dei due dadi)?
- 18/36
- 12/36
- 5/36
- 7/36
3
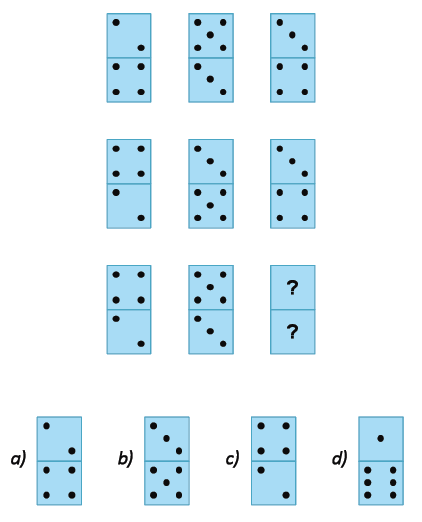
Quale tra le quattro proposte è la tessera mancante?
4
Un agricoltore coltiva nel suo orto solo 5 tipi differenti tipi verdure: fagioli, mais, fave, piselli, pomodori.
Ogni anno l’agricoltore pianta tre tipi di verdure solo con le seguenti regole:
- se in un anno pianta il mais, allora in quello stesso anno necessariamente pianta anche i fagioli;
- se in un anno pianta le fave, allora necessariamente l’anno seguente non le pianta;
- in ogni anno l’agricoltore pianta al massimo un tipo di verdura piantata nell’anno precedente.
Se l’agricoltore in un certo anno semina fagioli, fave e mais, dire quali delle seguenti semine può essere fatta due anni dopo.
- Fagioli, mais, piselli.
- Fagioli, fave, mais.
- Fagioli, fave, piselli.
- Fave, piselli, pomodori.
5
Si consideri la seguente moltiplicazione:
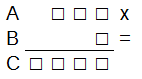
dove ciascuna delle cifre dei tre numeri A, B e C (indicate dal simbolo □) può valere solo 3, oppure 5, oppure 7.
Quali sono i tre numeri A, B e C?
6
Nove ragazzi (indicati con le prime nove lettere dell’alfabeto A, B, C, D, E, F, G, H, I) organizzano riunioni seduti attorno a un tavolo rotondo; nella prima riunione A è seduto nel posto numero 1, B nel 2 e così di seguito ordinatamente H nel posto 8 e I nel 9.
In questa prima riunione, A è seduto fra B e I.
Per le riunioni successive, decidono di cambiare di posto usando la regola descritta dalla seguente corrispondenza:
Così, A che nella prima riunione è al posto 1, nella seconda riunione andrà nel posto 4.
B che nella seconda riunione occupa il posto 7, nella terza occuperà il posto 8.
Trovare le posizioni PD, PE, PF, PG, PI occupate rispettivamente da D, E, F, G, I nella quinta riunione.
7
Per rispettare i tempi delle prenotazioni quando si devono consegnare delle pizze alle abitazioni poste ai numeri dispari di una stessa via, le pizze devono essere consegnate seguendo le istruzioni scritte usando un codice che specifica come spostarsi avanti (per esempio A2, per muoversi in avanti di due abitazioni) e indietro (per esempio I5, per tornare indietro di 5 abitazioni) lungo la via a partire da un punto specificato.
Un esempio di consegna di 4 pizze: se a partire dall’abitazione situata al numero 1 le istruzioni fossero descritte dalla seguente lista [A2, A1, I2], le consegne seguirebbero l’ordine descritto dalla seguente lista [1, 5, 7, 3] che indica i numeri civici (dispari) delle abitazioni cui effettuare le consegne.
Si devono consegnare 7 pizze. La prima pizza va consegnata all’abitazione situata al numero 1, le rimanenti vanno consegnate eseguendo le seguenti istruzioni: [A3, A4, I5, A6, I3, I4].
Trovare la lista L che contiene i numeri civici delle abitazioni disposti secondo l’ordine di consegna delle pizze.
8
Sono date due liste di numeri pari Lm, detta lista dei minori, e LM detta lista dei maggiori, come mostrato nel seguente esempio:
- Lm = [12, 14, 12, 22, 18, 24]
- LM = [26, 20, 16, 28, 30, 28, 32, 30, 30]
Un separatore per queste due liste è un numero dispari che sia maggiore di tutti i numeri della lista Lm e minore di tutti quelli della lista LM.
Poiché – come nell’esempio sopra riportato – alcuni numeri della prima lista sono maggiori di alcuni numeri della seconda, a ogni separatore ipotizzato S viene associato un errore dato dal numero di elementi di Lm maggiori di S più il numero di elementi di LM minori di S.
Nella tabella seguente sono riportati, ancora con riferimento al caso precedente, alcuni esempi di separatori e dei rispettivi errori.
Si dice separatore ottimale il numero dispari cui corrisponde l’errore minimo.
In questo esempio, il separatore ottimale è il numero 25.
Data la seguente coppia di liste:
- Lm = [2, 4, 6, 8, 6, 6, 8, 4, 2, 10, 10, 10, 8]
- LM = [12, 14, 12, 8, 10, 10, 8, 8, 6, 6, 4, 6, 10, 6]
Trovare il separatore ottimale S e il suo errore E.
9
Sul fianco di una montagna esistono numerose sorgenti.
L’acqua di una sorgente, che si suppone fluire in modo costante, può scorrere a valle attraverso uno o più rigagnoli.
Può avvenire che questi confluiscano in un punto in cui esiste una sorgente; in tal caso, la loro acqua si aggiunge a quella fornita da questa sorgente.
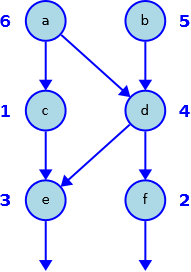
La situazione è quindi descrivibile con una rete: i nodi della rete rappresentano le sorgenti e gli archi rappresentano i rigagnoli. Si ipotizzi che i rigagnoli non possano incrociarsi fra di loro.
La situazione complessiva di un reticolo è descritta quindi da una sequenza di termini s(<sorgente>,<acqua>), che specificano la quantità di acqua in litri al minuto che sgorga da ogni sorgente, e da una sequenza di termini r(<sorgente1>,<sorgente2>), che specificano l’esistenza di un rigagnolo che esce dalla sorgente1 e confluisce nella sorgente2.
Se da una sorgente escono più rigagnoli, l’acqua si divide in parti uguali fra ciascuno di essi.
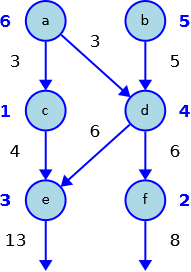A titolo di esempio, nella rete descritta dalle due sequenze:
- s(a,6), s(b,5), s(c,1), s(d,4), s(e,3), s(f,2)
- r(a,c), r(a,d), r(b,d), r(c,e),r(d,e), r(d,f)
e rappresentata in figura, la quantità d’acqua che esce dai nodi e, f risulta essere:
- e=13
- f=8.
Un reticolo è descritto dalle seguenti due sequenze:
- s(a,2), s(b,6), s(c,4), s(d,8), s(e,3), s(f,2), s(g,2), s(h,2), s(i,12), s(j,3), s(k,5), s(m,1)
- r(a,e), r(b,e), r(b,f), r(c,f), r(c,g), r(d,g), r(d,h), r(e,i), r(f,j), r(g,j), r(g,m), r(h,m), r(i,k), r(j,k), r(j,m)
Calcolare la quantità di acqua che esce dai nodi k e m.
10
Data una lista di numeri diversi, per esempio [1,5,2,4], è possibile alterare l’ordine dei suoi elementi scambiando di posto due cifre adiacenti.
Con mosse successive è quindi possibile spostare gli elementi della lista in modo da ottenere la permutazione ordinata crescente; in questo esempio, l’ordinamento si ottiene con due mosse:
[1,5,2,4] → [1,2,5,4] → [1,2,4,5].
La lista [2,5,4,3] può essere ordinata con tre mosse:
[2,5,4,3] → [2,4,5,3] → [2,4,3,5] → [2,3,4,5].
Date le seguenti liste
- L1 = [4,9,2,8,3,7],
- L2 = [2,1,4,3,6,5,9,7,10,8]
Trovare il numero minimo di mosse (N1 e N2 rispettivamente per L1 e L2) necessario per ottenere le corrispondenti permutazioni ordinate crescenti.
11
Date due liste L1 e L2 di caratteri – per esempio L1= [r,i,s,o,t,t,o] e L2= [p,r,e,s,t,o] – si definisce distanza di L1 da L2 il numero minimo di “mosse” da eseguire su L1 per renderla uguale a L2, dove ogni mossa può essere una delle seguenti tre operazioni:
- sostituzione di un carattere di L1 con altro carattere;
- inserimento di un nuovo carattere in L1;
- cancellazione di un carattere di L1.
Ad esempio, L1 può essere trasformata in L2 con 13 mosse: infatti con 7 cancellazioni, L1 diventa uguale alla lista vuota [ ] e con 6 inserimenti successivi (dei 6 caratteri p r e s t o) la lista vuota diventa uguale a L2.
Ma L1 può essere trasformata in L2 anche con solo 4 mosse: inserendo in prima posizione il carattere p, sostituendo il carattere i con il caratteree, cancellando il primo carattere o e uno dei due caratteri t.
La distanza di L1 da L2 è quindi 4.
Trovare la distanza D tra le due liste L1=[r,p,a,l,z,m,g] e L2=[b,r,x,a,m,g].
12
Il termine a(<nodo1>,<nodo2>,<distanza>) descrive un tratto stradale che unisce nodo1 e nodo2, con la indicazione della relativa distanza (in Km).
Sia dato il grafo stradale composto dai seguenti tratti:
e rappresentato in figura
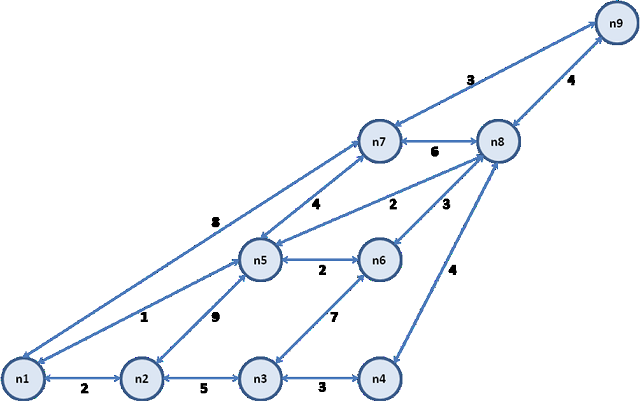
Un percorso tra due nodi viene descritto con la lista dei nodi che lo compongono ordinati dal nodo di partenza al nodo di arrivo.
Di ciascun percorso può naturalmente essere calcolata la lunghezza totale in Km.
Per esempio, il percorso L = [n1,n7,n8,n6] ha una lunghezza K di 17 Km.
Trovare il numero N di percorsi diversi che partono dal nodo n2, terminano nel nodo n9 e passano una sola volta per tutti i nodi del grafo; tra questi percorsi fornire la lista L1 di quello più breve e la lista L2 di quello più lungo.
13
Alcuni ragazzi decidono di costruire un ipertesto multimediale sugli avvenimenti storici significativi della loro regione.
Per organizzare il progetto, dividono il lavoro in 9 attività e assegnano ogni attività a un gruppo di loro.
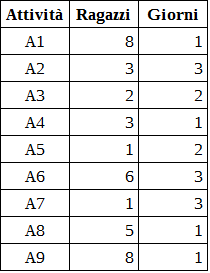La tabella che segue descrive le 9 attività (indicate rispettivamente con le sigle A1, A2, …, A9) riportando per ciascuna di esse il numero di ragazzi assegnato e il numero di giorni per completarla.
Per esempio, la coppia (A1,A3) indica che l’attività A3 può cominciare solo quando è terminata l’attività A1.
L’attività che non ha nessuna antecedente è la prima, quella che non compare mai come antecedente è l’ultima.
Se un’attività ha più antecedenti, può essere iniziata solo quando tutte le antecedenti sono terminate.
Con le sequenzialità descritte dal seguente elenco: (A1,A2) (A1,A3) (A1,A4) (A2,A7) (A2,A8) (A3,A6) (A3,A8) (A4,A5) (A5,A8) (A6,A9) (A7,A9) (A8,A9) e assumendo che l’attività A1 inizi il giorno 1:
- trovare il numero N di giorni necessari per completare il progetto, tenuto presente che alcune attività possono essere svolte in parallelo e che ogni attività deve iniziare il prima possibile (nel rispetto delle sequenzialità);
- trovare il numero X1 che individua il giorno in cui lavora il maggior numero M1 di ragazzi e calcolare M1;
- trovare il numero X2 del giorno in cui lavora il minor numero M2 di ragazzi e calcolare M2;
- supponendo che la retribuzione media giornaliera per ragazzo sia di 90 euro, calcolare il costo complessivo S del progetto.