Utilizza i moduli … per …
- fractions, mantenere formali i risultati delle operazioni con le frazioni
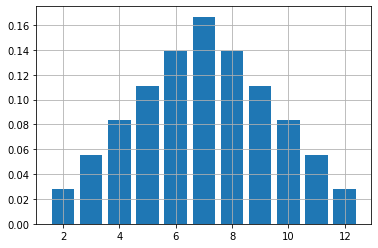
- matplotlib, rappresentare graficamente la distribuzione delle probabilità
- math, radice quadrata
from fractions import Fraction as F # Fraction()
import matplotlib.pyplot as plt # plot()
import math # sqrt()
N = 13*[0] # Conteggio degli esiti del lancio di due dadi
for d1 in range(1, 7):
for d2 in range(1,7):
dadi=d1+d2
N[dadi] += 1
X = list(range(2, 13))
P = [] # Probabilità: frequenze assolute
for x in X:
p=F(N[x], 36)
P.append(p)
plt.bar(X, P) # Grafico a barre verticali
plt.grid()
plt.show()
print(" x | p(x)") # Tabella
print("----|------")
for x, p in zip(X, P):
print(" %2i | %s" %(x, p))
Risultato
x | p(x)
----|------
2 | 1/36
3 | 1/18
4 | 1/12
5 | 1/9
6 | 5/36
7 | 1/6
8 | 5/36
9 | 1/9
10 | 1/12
11 | 1/18
12 | 1/36
Il resto del codice esegue i calcoli
media = 0
media_quadrati = 0
for p, x in zip(P, X):
media += p*x
media_quadrati += p*x**2
varianza_1 = media_quadrati-media**2
print("Media = %5s %10.6f" %(media , media ))
print("Media dei quadrati = %5s %10.6f" %(media_quadrati, media_quadrati))
print("Varianza (1) = %5s %10.6f" %(varianza_1 , varianza_1 ))
scarto_medio_assoluto = 0
devianza = 0
varianza_2 = 0
for p, x in zip(P, X):
scarto_medio_assoluto += p*abs(media-x)
devianza += (media-x)**2
varianza_2 += p*(media-x)**2
print("Scarto medio assoluto = %5s %10.6f" %(scarto_medio_assoluto, scarto_medio_assoluto))
print("Devianza = %5s %10.6f" %(devianza , devianza ))
print("Varianza (2) = %5s %10.6f" %(varianza_2 , varianza_2 ))
deviazione_standard = math.sqrt(varianza_2)
deviazione_standard_relativa = deviazione_standard/abs(media)
print("Deviazione standard =", deviazione_standard )
print("Deviazione standard rel. =", deviazione_standard_relativa)
Risultati
Media = 7 7.000000
Media dei quadrati = 329/6 54.833333
Varianza (1) = 35/6 5.833333
Scarto medio assoluto = 35/18 1.944444
Devianza = 110 110.000000
Varianza (2) = 35/6 5.833333
Deviazione standard = 2.41522945769824
Deviazione standard rel. = 0.3450327796711771
Riepilogo
![]()
![]()
![]()
![]()
![]()
collections
SymPy
I moduli … permettono di …
- collections, conteggiare gli esiti di due dadi con l’oggetto Counter
- sympy, mantenere formale anche la radice quadrata
import collections # Counter()
import matplotlib.pyplot as plt
import sympy as sp # Rational(), sqrt()
DADO = list(range(1, 7))
DADI = [d1+d2 for d1 in DADO for d2 in DADO]
COUNT = collections.Counter(DADI)
X = COUNT.keys()
P = [sp.Rational(count, 36) for count in COUNT.values()]
plt.bar(X, P)
plt.grid()
plt.show()
print(" x | p(x)")
print("----|------")
for x, p in zip(X, P):
print(" %2i | %s" %(x, p))
e con lo stesso codice precedente ottenere anche la deviazione standard in formato leggibile
![]()
![]()