Compleanni coincidenti

di

Olimpiadi Italiane di Statistica 2011 E.M. – 2

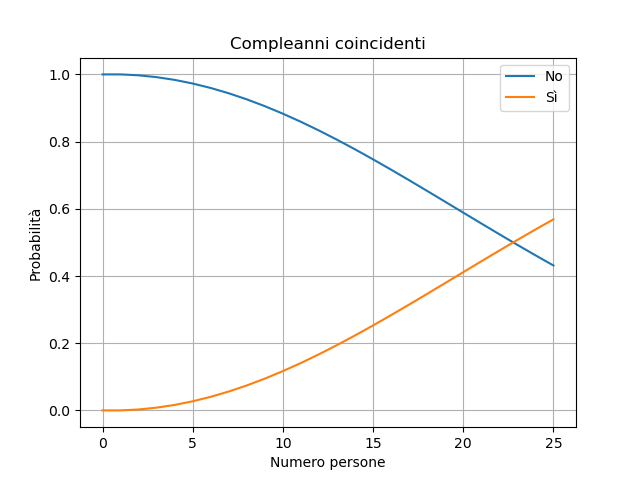
Qual è la probabilità che in una classe di 25 alunni, almeno due compiano gli anni lo stesso giorno?

Con formula

Vedi la discussione

La probabilità con 25 persone è superiore al 50%

import matplotlib.pyplot as plt

PERSONE=25

ANNO=365

pNo =(PERSONE+1)*[0]
pSì =(PERSONE+1)*[0]
pNo[0]=1
pSì[0]=0
pNo[1]=1
pSì[1]=0
for n in range(2, PERSONE+1):
    pNo[n] = pNo[n-1]*(ANNO-(n-1))/ANNO
    pSì[n] = 1-pNo[n]

for n in range(0, PERSONE+1):
    print("%2i %f %f" %(n, pNo[n],pSì[n]))

N=range(0, PERSONE+1)
    
plt.grid()
plt.plot(N,pNo)
plt.plot(N,pSì)
plt.legend(["No", "Sì"])
plt.title("Compleanni coincidenti")
plt.xlabel("Numero persone")
plt.ylabel("Probabilità")

plt.show()

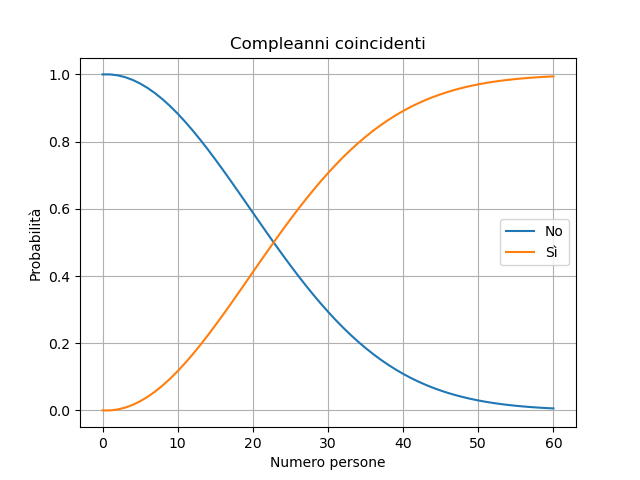
Aumentando il numero di persone a 60 si può notare che la probabilità è molto vicina al 100%

Metodo probabilistico

Genera 25 giorni di nascita casuali e controlla se ci sono coincidenze, ripete 1000 volte

import random                           # randint()

INCONTRI=1000                           # Numero di incontri
PERSONE =25                             # Numero di persone presenti

coincidenze=0
for incontro in range(INCONTRI):
    giorni=set()                        # Insieme vuoto
    for compleanno in range(PERSONE):
        giorno=random.randint(1, 365)   # Un giorno a caso (da 1 a 365)
        giorni.add(giorno)              # Aggiunto all'insieme dei giorni
    if(len(giorni) < PERSONE):          # Se i giorni sono meno delle PERSONE
        coincidenze += 1 

freq=coincidenze/INCONTRI               # Frequenza -> probabilità
print(freq)