Numero di Eulero con serie – Programmare con Python

Vedi: math.e, math.factorial(), Fattoriale

Serie

$\displaystyle e=\sum_{n=0}^{+\infty}\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\dots=1+1+\frac{1}{2}+\frac{1}{6}+\dots$

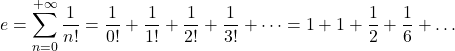
import math  # math.factorial()
 
PASSI=10
 
Sn=0
for n in range(PASSI):
    fn  = math.factorial(n)
    an  = 1/fn
    Sn += an
 
    print("%i | %6i | %12.10f | %12.10f"%(n, fn, an, Sn))

Output

0 |      1 | 1.0000000000 | 1.0000000000
1 |      1 | 1.0000000000 | 2.0000000000
2 |      2 | 0.5000000000 | 2.5000000000
3 |      6 | 0.1666666667 | 2.6666666667
4 |     24 | 0.0416666667 | 2.7083333333
5 |    120 | 0.0083333333 | 2.7166666667
6 |    720 | 0.0013888889 | 2.7180555556
7 |   5040 | 0.0001984127 | 2.7182539683
8 |  40320 | 0.0000248016 | 2.7182787698
9 | 362880 | 0.0000027557 | 2.7182815256

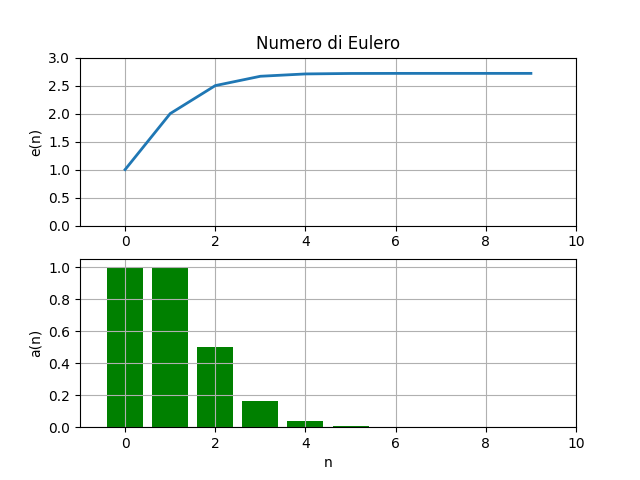
matpolotlib

import math
import matplotlib.pyplot as plt
 
PASSI = 10
 
N  = []
AN = []
SN = []
Sn = 0
for n in range(PASSI):
    an  = 1/math.factorial(n)
    Sn += an

    print(n, an, Sn)
 
    N.append(n)
    AN.append(an) 
    SN.append(Sn)

plt.subplot(2, 1, 1)
plt.grid()
plt.plot(N, SN, linewidth="2")
plt.title("Numero di Eulero")
plt.xlim(-1, PASSI) 
plt.ylim(0, 3) 
plt.ylabel("e(n)")

plt.subplot(2, 1, 2)
plt.bar(N, AN, color="green")
plt.grid()
plt.xlabel("n")
plt.xlim(-1, PASSI) 
plt.ylabel("a(n)")

plt.show()

fractions

Ottieni una successione di frazioni che converge al numero di Eulero!

import fractions
import math

Sn=0
for n in range(10):
    fn = math.factorial(n)
    an = fractions.Fraction(1, fn)
    Sn += an
    print("%d | %6d | %8s | %12s | %.10f" %(n, fn, an, Sn, Sn))

Output

0 |      1 |        1 |            1 | 1.0000000000
1 |      1 |        1 |            2 | 2.0000000000
2 |      2 |      1/2 |          5/2 | 2.5000000000
3 |      6 |      1/6 |          8/3 | 2.6666666667
4 |     24 |     1/24 |        65/24 | 2.7083333333
5 |    120 |    1/120 |       163/60 | 2.7166666667
6 |    720 |    1/720 |     1957/720 | 2.7180555556
7 |   5040 |   1/5040 |      685/252 | 2.7182539683
8 |  40320 |  1/40320 | 109601/40320 | 2.7182787698
9 | 362880 | 1/362880 |  98641/36288 | 2.7182815256