Operazioni con vettori – Programmare con Python

Considera tre vettori della stessa lunghezza

vettA=[2,7,1,0,1,9,9,5]

vettB=[1,2,0,4,1,9,9,7]

vettC=[1,8,0,5,1,9,9,9]

Prodotto per uno scalare

def scalare(k, v):

n=len(v)

w=[]

for i in range(n):

w.append(k*v[i])

return w

vettD=scalare(2, vettA) # 2*[2,7,1,0,1,9,9,5] = [4,14,2, 0,2,18,18,10]

vettD=scalare(3, vettB) # 3*[1,2,0,4,1,9,9,7] = [3, 6,0,12,3,27,27,21]

vettD=scalare(4, vettC) # 4*[1,8,0,5,1,9,9,9] = [4,32,0,20,4,36,36,36]

Somma

def somma(v1,v2):

n=len(v1)

w=[]

for i in range(n):

w.append(v1[i]+v2[i])

return w

vettD=somma(vettA, vettB) # [2,7,1,0,1,9,9,5]+[1,2,0,4,1,9,9,7] = [3, 9,1,4,2,18,18,12]

vettE=somma(vettA, vettC) # [2,7,1,0,1,9,9,5]+[1,8,0,5,1,9,9,9] = [3,15,1,5,2,18,18,14]

vettF=somma(vettB, vettC) # [1,2,0,4,1,9,9,7]+[1,8,0,5,1,9,9,9] = [2,10,0,9,2,18,18,16]

Differenza

...

Prodotto scalare

Formula

$a_1\cdot b_1+a_2\cdot b_2+ \ \dots \ +a_n\cdot b_n$

def prodScalare(v1,v2):

n=len(v1)

somma=0

for i in range(n):

somma += v1[i]*v2[i]

return somma

ps1=prodScalare(vettA, vettB) # [2,7,1,0,1,9,9,5]*[1,2,0,4,1,9,9,7]

# = 2*1+7*2+1*0+0*4+1*1+9*9+9*9+5*7

# = 214

ps2=prodScalare(vettA, vettC) # ... = 266

ps3=prodScalare(vettB, vettC) # ... = 263

Norma di un vettore

Formula

$\sqrt {a_1^2+a_2^2+ \ \dots \ +a_n^2}$

def norma(v):

n=len(v)

somma=0

for i in range(n):

somma += v[i]**2

return math.sqrt(somma)

def norma(v): # Più breve

return math.sqrt(prodScalare(v,v)) # Utilizza prodotto scalare

n1=norma(vettA) # | [2,7,1,0,1,9,9,5] |

# = RADQ(2*2+7*7+1*1+0*0+1*1+9*9+9*9+5*5)

# = RADQ(4+49+1+0+1+81+81+25)

# = RADQ(242)

# = 15.5563...

n2=norma(vettB) # ... = 15.2643...

n3=norma(vettC) # ... = 18.2756...

I due vettori sono compatibili?

Alcune funzioni hanno senso solo se i due vettori sono compatibili (hanno la stessa lunghezza…)

Si potrebbe aggiungere un controllo preventivo

def funzione(v1, v2):

n1=len(v1)

n2=len(v2)

if(n1 != n2): return

...

Prodotto vettoriale

Da Wikipedia

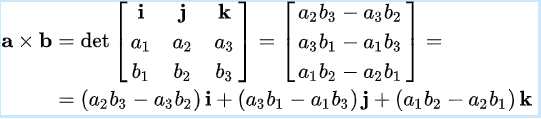
def prodVett(a,b): # a e b sono vettori di dimensione 3

c=3*[0]

c[0]=a[1]*b[2]-a[2]*b[1] # Indici 0,1,2 invece di 1,2,3

c[1]=a[2]*b[0]-a[0]*b[2]

c[2]=a[0]*b[1]-a[1]*b[0]

return c

vettA=[1,0,0]

vettB=[0,1,0]

vettC=[0,0,1]

vett1=prodVett(vettA,vettA) # [0, 0, 0]

vett2=prodVett(vettA,vettB) # [0, 0, 1]

vett3=prodVett(vettA,vettC) # [0,-1, 0]

vett4=prodVett(vettB,vettA) # [0, 0,-1]