import math
QUANTE = 10
r = 1 # Per semplificare...
n = 4 # Il primo poligono è un QUADRATO
l = math.sqrt(2) # Il lato del 1° poligono è ...
p = n*l # n*lato
pi = p/(2*r) # Perimetro/Diametro
a = math.sqrt(r*r-(l/2)**2) # "Ipotenusa..."
d = r-a # ...
print(pi) # 1° approssimazione
for passo in range(1,QUANTE):
n = 2*n # Il numero di lati raddoppia
l = math.sqrt((l/2)**2+d**2) # "Ipotenusa..."
p = n*l # ...
pi = p/(2*r) # ...
a = math.sqrt(r*r-(l/2)**2) # ...
d = r-a # ...
print(pi) # Approssimazioni successive
Si ottiene la sequenza
2.8284271247461903
3.0614674589207187
3.121445152258053
3.1365484905459398
3.1403311569547534
3.1412772509327733
3.1415138011443013
3.141572940367092
3.14158772527716
3.1415914215112
SymPy
Con la stessa tecnica utilizzata partendo da un esagono
import math
import sympy as sp # Modulo SymPy
QUANTE = 5 # SCEGLI QUANTE APPROSSIMAZIONI
sp.init_printing() # Abilita pprint()
r = sp.symbols('r') # Raggio della circonferenza
n = sp.symbols('n') # Numero di lati del poligono
l = sp.symbols('l') # Lato del poligono
p = sp.symbols('p') # Perimetro del poligono
pi = sp.symbols('pi') # Approssimazione di pi greco
a = sp.symbols('a') # Apotema del poligono
d = sp.symbols('d') # Differenza tra il raggio e l'apotema
n = 4 # Il primo poligono è un quadrato
l = sp.sqrt(2)*r # Il lato è uguale a ...
p = n*l # n*lato
pi = p/(2*r) # Perimetro/Diametro
a = sp.sqrt(r*r-(l/2)**2) # "Ipotenusa..."
d = r-a # ...
PIGRECO = sp.simplify(pi.subs(r, 1)) # Sostituisce e semplifica
sp.pprint(PIGRECO) # Stampa la formula in forma comprensibile
print(sp.latex(PIGRECO)) # in LaTeX
print(PIGRECO.evalf(20)) # 20 cifre dopo la virgola
for passo in range(1,QUANTE):
n = 2*n # Il numero di lati raddoppia
l = sp.sqrt((l/2)**2+d**2) # "Ipotenusa..."
p = n*l # ...
pi = p/(2*r) # ...
a = sp.sqrt(r*r-(l/2)**2) # ...
d = r-a # ...
PIGRECO = sp.simplify(pi.subs(r, 1))
sp.pprint(PIGRECO)
print(sp.latex(PIGRECO))
print(PIGRECO.evalf(20))
Si ottiene
2⋅√2
2 \sqrt{2}
2.8284271247461900976
________
4⋅╲╱ 2 - √2
4 \sqrt{2 - \sqrt{2}}
3.0614674589207181738
________________
╱ ________
8⋅╲╱ 2 - ╲╱ √2 + 2
8 \sqrt{2 - \sqrt{\sqrt{2} + 2}}
3.1214451522580522856
_________________________
╱ ________________
╱ ╱ ________
16⋅╲╱ 2 - ╲╱ ╲╱ √2 + 2 + 2
16 \sqrt{2 - \sqrt{\sqrt{\sqrt{2} + 2} + 2}}
3.1365484905459392638
___________________________________
╱ _________________________
╱ ╱ ________________
╱ ╱ ╱ ________
32⋅╲╱ 2 - ╲╱ ╲╱ ╲╱ √2 + 2 + 2 + 2
32 \sqrt{2 - \sqrt{\sqrt{\sqrt{\sqrt{2} + 2} + 2} + 2}}
3.1403311569547529123
Utilizzando le codifiche LaTeX (con qualche commutazione)
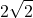
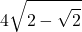
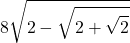
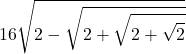
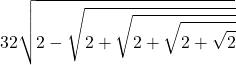
- …