1
Numero fisso di passi (1 + 5)
def f(x): return 1/3*x**3-5/3*x**2+2*x
a = 2.5
b = 4
fa = f(a)
fb = f(b)
for i in range(5):
m = (a+b)/2
fm = f(m)
print("%10.6f %10.6f %10.6f %10.6f %10.6f %10.6f" %(a,m,b, fa,fm,fb))
if(fm == 0):
print("Successo!")
break
elif(fa*fm > 0):
a = m
fa = fm
elif(fb*fm > 0):
b = m
fb = f(m)
else:
print("Errore...")
break
print()
print("La soluzione è", m)
2
Il numero di passi dipende dall’errore
def f(x): return 1/3*x**3-5/3*x**2+2*x
a = 2.5
b = 4
fa = f(a)
fb = f(b)
ERRORE = 0.01
errore = 1.0
while(errore > ERRORE):
m = (a+b)/2
fm = f(m)
errore = b-m
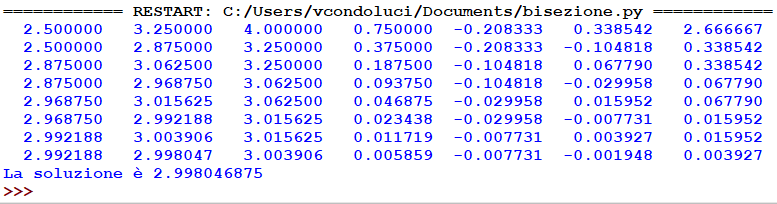
print("%10.6f %10.6f %10.6f %10.6f %10.6f %10.6f %10.6f" %(a,m,b, errore, fa,fm,fb))
if(fm == 0):
print("Successo!")
break
elif(fa*fm > 0):
a = m
fa = fm
elif(fb*fm > 0):
b = m
fb = f(m)
else:
print("Errore...")
break
print()
print("La soluzione è", m)
import matplotlib.pyplot as plt
def f(x): return 1/3*x**3-5/3*x**2+2*x
PASSI=7
I=range(PASSI)
A=[]
B=[]
M=[]
a =2.5
b =4
fa=f(a)
fb=f(b)
for i in range(PASSI):
m = (a+b)/2
fm = f(m)
errore = b-m
print("%10.6f %10.6f %10.6f %10.6f %10.6f %10.6f %10.6f" %(a,m,b, errore, fa,fm,fb))
A.append(a)
B.append(b)
M.append(m)
if(fm == 0):
print("Successo!")
break
elif(fa*fm > 0):
a = m
fa = fm
elif(fb*fm > 0):
b = m
fb = fm
else:
print("Errore...")
break
print()
print("La soluzione è", m)
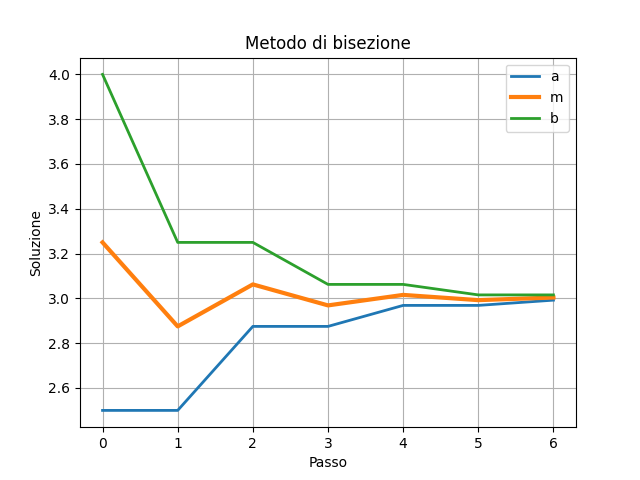
plt.plot(I, A, label="a", linewidth="2")
plt.plot(I, M, label="m", linewidth="3")
plt.plot(I, B, label="b", linewidth="2")
plt.title("Metodo di bisezione")
plt.xlabel("Soluzione")
plt.ylabel("Passo")
plt.grid(True)
plt.legend()
plt.show()
Forse è più chiaro con la soluzione come ascissa?
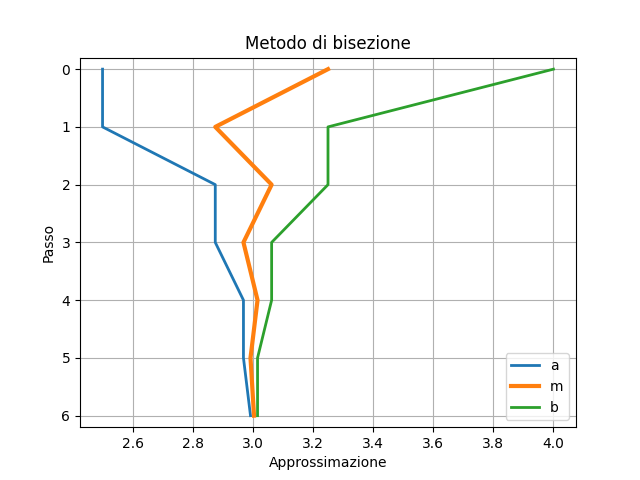
Nella funzione plt.plot() Inserisci I dopo A/B/M …
...
plt.plot(A, I, label="a", linewidth="2")
plt.plot(M, I, label="m", linewidth="3")
plt.plot(B, I, label="b", linewidth="2")
...