Analisi di un dado – Programmare con Python

Vedi la discussione

Le sei facce di un dado sono equiprobabili

$\displaystyle p(i) = \frac{1}{6}, i=1,...,6$

Sia X la variabile casuale “punti realizzati lanciando un dado”, allora

$\displaystyle M(X) = \sum_{i=1}^6 p_i\cdot x_i$

$\displaystyle M(X^2) = \sum_{i=1}^6 p_i\cdot x_i^2$

$\displaystyle var(X) = M(X^2) - M(X)^2$

$\displaystyle \delta(X) = \sum_{i=1}^6 p_i\cdot(m - x_i)$

$\displaystyle dev(X) = \sum_{i=1}^6 (m - x_i)^2$

$\displaystyle var(X) = \sum_{i=1}^6 p_i\cdot(m - x_i)^2$

$\displaystyle \sigma(X) = \sqrt{var(X)}$

$\displaystyle \sigma^*(X) = \frac { \sigma(X) } { M(X) }$

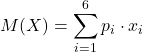
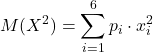
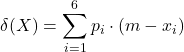
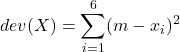
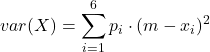
Il modulo fractions permette di operare con le frazioni in modo simbolico, cioè sono trattate formalmente fino alla fine dei calcoli.

fractions

La lista X contiene i possibili esiti da 1 a 6.
La lista P contiene le probabilità, come frazione 1/6.

import fractions  # Fractions
import math       # sqrt()

X = list(range(1, 7))
P = 6*[fractions.Fraction(1,6)] 

print("+---+------+")
print("| x | p(x) |")
print("+---+------+")
for x, p in zip(X, P):
    print("| %i |  %s |" %(x, p))
print("+---+------+")

+---+------+
| x | p(x) | 
+---+------+ 
| 1 |  1/6 | 
| 2 |  1/6 | 
| 3 |  1/6 | 
| 4 |  1/6 | 
| 5 |  1/6 | 
| 6 |  1/6 |
+---+------+

Con i calcoli successivi sarà possibile leggere i risultati come frazioni e come numeri decimali

media          = 0
media_quadrati = 0

for p, x in zip(P, X):
    media          += p*x
    media_quadrati += p*x**2

varianza_1 = media_quadrati-media**2
print("Media              = %5s %10.6f" %(media         , media         ))
print("Media dei quadrati = %5s %10.6f" %(media_quadrati, media_quadrati))
print("Varianza  (1)      = %5s %10.6f" %(varianza_1    , varianza_1    ))

#-------------------------------------------------------------------------

scarto_medio_assoluto = 0
devianza              = 0
varianza_2            = 0
for p, x in zip(P, X):
    scarto                 = media-x
    scarto_medio_assoluto += p*abs(scarto)
    devianza              += scarto**2  
    varianza_2            += p*scarto**2

print("Scarto medio assoluto = %5s %10.6f" %(scarto_medio_assoluto, scarto_medio_assoluto))
print("Devianza              = %5s %10.6f" %(devianza             , devianza             ))
print("Varianza (2)          = %5s %10.6f" %(varianza_2           , varianza_2           ))

#-------------------------------------------------------------------------

deviazione_standard          = math.sqrt(varianza_2)
deviazione_standard_relativa = deviazione_standard/abs(media)
print("Deviazione standard      =", deviazione_standard         )
print("Deviazione standard rel. =", deviazione_standard_relativa)

Per ottenere

Media              =   7/2   3.500000 
Media dei quadrati =  91/6  15.166667 
Varianza (1)       = 35/12   2.916667

Scarto medio assoluto =   3/2  1.500000 
Devianza              =  35/2 17.500000 
Varianza (2)          = 35/12  2.916667


Deviazione standard      = 1.707825127659933 
Deviazione standard rel. = 0.48795003647426655

Osserva i risultati espressi come frazioni

$\displaystyle M(X) = \frac{7}{2}$

$\displaystyle M(X^2) = \frac{91}{6}$

$\displaystyle \delta(X) = \frac{3}{2}$

$\displaystyle dev(X) = \frac{35}{2}$

$\displaystyle var(X) = \frac{35}{12}$

Purtroppo… la deviazione standard richiede la radice quadrata che annulla l’intervanto di fractions.

SymPy

Il modulo sympy permette di operare in modo simbolico anche con la radice quadrata e quindi arrivare fino alla fine

import sympy as sp # Rational(), sqrt()

X = list(range(1, 7))     # Esiti
P = 6*[sp.Rational(1, 6)] # Probabilità

print("+---+------+")
print("| x | p(x) |")
print("+---+------+")
for x, p in zip(X, P):
    print("| %i |  %s |" %(x, p))
print("+---+------+")

media          = 0 
media_quadrati = 0 
for p, x in zip(P, X):    
    media          += p*x    
    media_quadrati += p*x**2 
    varianza_1 = media_quadrati-media**2

print("Media              = %5s %10.6f" %(media         , media         )) 
print("Media dei quadrati = %5s %10.6f" %(media_quadrati, media_quadrati)) 
print("Varianza  (1)      = %5s %10.6f" %(varianza_1    , varianza_1    ))


scarto_medio_assoluto = 0 
devianza              = 0 
varianza_2            = 0 

for p, x in zip(P, X): 
    scarto = (media-x)    
    scarto_medio_assoluto += p*abs(scarto)    
    devianza              += scarto**2     
    varianza_2            += p*scarto**2 

print("Scarto medio assoluto = %5s %10.6f" %(scarto_medio_assoluto, scarto_medio_assoluto)) 
print("Devianza              = %5s %10.6f" %(devianza             , devianza             )) 
print("Varianza (2)          = %5s %10.6f" %(varianza_2           , varianza_2           ))


deviazione_standard          = sp.sqrt(varianza_2) 
deviazione_standard_relativa = deviazione_standard/abs(media) 

print("Deviazione standard      = %12s %10.6f" %(deviazione_standard         , deviazione_standard         )) 
print("Deviazione standard rel. = %12s %10.6f" %(deviazione_standard_relativa, deviazione_standard_relativa))

Per ottenere

+---+------+
| x | p(x) | 
+---+------+ 
| 1 |  1/6 | 
| 2 |  1/6 | 
| 3 |  1/6 | 
| 4 |  1/6 | 
| 5 |  1/6 | 
| 6 |  1/6 |
+---+------+

Media              =   7/2   3.500000 
Media dei quadrati =  91/6  15.166667 
Varianza (1)       = 35/12   2.916667

Scarto medio assoluto =   3/2   1.500000 
Devianza              =  35/2  17.500000 
Varianza (2)          = 35/12   2.916667

Deviazione standard      =  sqrt(105)/6  1.707825 
Deviazione standard rel. = sqrt(105)/21  0.487950

E quindi…

$\displaystyle M(X) = \frac{7}{2}$

$\displaystyle M(X^2) = \frac{91}{6}$

$\displaystyle \delta(X) = \frac{3}{2}$

$\displaystyle dev(X) = \frac{35}{2}$

$\displaystyle var(X) = \frac{35}{12}$

$\displaystyle \sigma(X) = \frac{\sqrt{105}}{6}$

$\displaystyle \sigma^*(X) = \frac{\sqrt{105}}{21}$

Osserva: le frazioni sono razionalizzate.