Analisi di UN dado

di

Ciascuna faccia del dado ha probabilità teorica 1/6 (16,6… %)

Sia X la variabile casuale “punti realizzati lanciando un dado”, allora

\displaystyle x_i\displaystyle p_i\displaystyle p_i\cdot x_i\displaystyle x_i^2\displaystyle p_i\cdot x_i^2\displaystyle x_i-m\displaystyle p_i (x{i}-m)\displaystyle |x_i-m|\displaystyle p_i\cdot |x_i-m|\displaystyle (x_i-m)^2\displaystyle p_i\cdot (x_i-m)^2
1\displaystyle \frac{1}{6}\displaystyle \frac{1}{6}1\displaystyle \frac{1}{6}\displaystyle -\frac{5}{2}\displaystyle -\frac{5}{12}\displaystyle \frac{5}{2}\displaystyle \frac{5}{12}\displaystyle \frac{25}{4}\displaystyle \frac{25}{24}
2\displaystyle \frac{1}{6}\displaystyle \frac{1}{3}4\displaystyle \frac{2}{3}\displaystyle -\frac{3}{2}\displaystyle -\frac{1}{4}\displaystyle \frac{3}{2}\displaystyle \frac{1}{4}\displaystyle \frac{9}{4}\displaystyle \frac{3}{8}
3\displaystyle \frac{1}{6}\displaystyle \frac{1}{2}9\displaystyle \frac{3}{2}\displaystyle -\frac{1}{2}\displaystyle -\frac{1}{12}\displaystyle \frac{1}{2}\displaystyle \frac{1}{12}\displaystyle \frac{1}{4}\displaystyle \frac{1}{24}
4\displaystyle \frac{1}{6}\displaystyle \frac{2}{3}16\displaystyle \frac{8}{3}\displaystyle \frac{1}{2}\displaystyle \frac{1}{12}\displaystyle \frac{1}{2}\displaystyle \frac{1}{22}\displaystyle \frac{1}{4}\displaystyle \frac{1}{24}
5\displaystyle \frac{1}{6}\displaystyle \frac{5}{6}25\displaystyle \frac{25}{6}\displaystyle \frac{3}{2}\displaystyle \frac{1}{4}\displaystyle \frac{3}{2}\displaystyle \frac{1}{4}\displaystyle \frac{9}{4}\displaystyle \frac{3}{8}
6\displaystyle \frac{1}{6}1366\displaystyle \frac{5}{2}\displaystyle \frac{5}{12}\displaystyle \frac{5}{2}\displaystyle \frac{5}{12}\displaystyle \frac{25}{4}\displaystyle \frac{25}{24}
211\displaystyle \frac{7}{2}91\displaystyle \frac{91}{6}009\displaystyle \frac{3}{2}\displaystyle \frac{35}{2}\displaystyle \frac{35}{12}
  \displaystyle M(X) \displaystyle M(X^2)  \displaystyle \delta(X)\displaystyle dev(X)\displaystyle var(X)

Osserva

  \displaystyle \sum_i x_i= 21
  \displaystyle \sum_i p_i= 1
Media\displaystyle M(X)= \displaystyle \sum_i p_i\cdot x_i= \displaystyle \frac{7}{2}= 3,5
  \displaystyle \sum_i x_i^2= 91
Media dei quadrati\displaystyle M(X^2)= \displaystyle \sum_ip_i\cdot x_i^2= \displaystyle \frac{91}{6}= 15,1666…
  \displaystyle \sum _{i} (x_{i}-m)= 0
Valore medio dello scarto dalla media\displaystyle \sum_{i} p_i (x{i}-m)= 0
  \displaystyle \sum_{i} |x_{i}-m|}= 9
Scarto medio assoluto\displaystyle \delta(X)= \displaystyle \sum _{i}p_i|x_{i}-m|}= \displaystyle \frac{3}{2}= 1,5
Devianza\displaystyle dev(x)= \displaystyle \sum_{i}(x_i-m)^2= \displaystyle \frac{35}{2}= 17,5
Varianza
Valore medio dello scarto al quadrato		\displaystyle var(X)= \displaystyle \sum_i p_i(x_i-m)^2= \displaystyle \frac{35}{12}= 2,9166…
Deviazione standard
Scarto quadratico medio		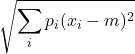\sigma (X)= \displaystyle \sqrt{\sum_i p_i(x_i-m)^2}= \displaystyle \sqrt{\frac{35}{12}}= 1,7078…
Deviazione standard relativa
Coefficiente di variazione		\displaystyle \sigma^{*}(X)= \displaystyle \frac{\sigma(X)}{|M(X)|}= \displaystyle \sqrt{\frac{35}{12}}\cdot \frac{2}{7}= 0,48795…
Varianzavar(X)= \displaystyle M(X^2)-[M(X)]^2= \displaystyle \frac{91}{6}- \left(\frac{7}{2}\right)^2 = \displaystyle \frac{35}{12}= 2,9166…