1
Esegue 5 passi dell’algoritmo e visualizza la sequenza delle approssimazioni.
n = 256
x = n/2
for i in range(5):
x = (x + n/x) / 2
print(i, ':', x)
0 : 65.0
1 : 34.46923076923077
2 : 20.94807220229001
3 : 16.584383571973717
4 : 16.010295955761958
Questa prima versione evidenzia la semplicità e l’efficienza dell’algoritmo!
Con le versioni successive l’algoritmo risulterà più esplicito.
2
Evidenzia che: date due approssimazioni, la loro media è un’approssimazione migliore…
n = 256
xM = n/2
for i in range(5):
xA = xM
xB = n / xA
xM = (xA + xB) / 2
print("%d : %10f %10f %10f"
%(i, xA, xB, xM))
0 : 128.000000 2.000000 65.000000
1 : 65.000000 3.938462 34.469231
2 : 34.469231 7.426914 20.948072
3 : 20.948072 12.220695 16.584384
4 : 16.584384 15.436208 16.010296
3
Input da tastiera di n e numero passi
...
4
Valutazione dell’errore assoluto
n = ...
p = ...
xM = n/2
for i in range(p):
xA = xM
xB = n / xA
xM = (xA + xB) / 2
eA = abs(xA - xM)
print("%i : %10f %10f %10f %10f"
%(i, xA, xB, xM, eA))
0 : 128.000000 2.000000 65.000000 63.000000
1 : 65.000000 3.938462 34.469231 30.530769
2 : 34.469231 7.426914 20.948072 13.521159
3 : 20.948072 12.220695 16.584384 4.363689
4 : 16.584384 15.436208 16.010296 0.574088
5
Valutazione dell’errore assoluto e dell’errore relativo
n = ...
p = ...
xM = n/2
for i in range(p):
xA = xM
xB = n / xA
xM = (xA + xB) / 2
eA = abs(xA - xM)
eR = eA / xM
print("%i : %10f %10f %10f %10f %10f"
%(i, xA, xB, xM, eA, eR))
0 : ... ... 65.000000 63.000000 0.969231
1 : ... ... 34.469231 30.530769 0.885740
2 : ... ... 20.948072 13.521159 0.645461
3 : ... ... 16.584384 4.363689 0.263120
4 : ... ... 16.010296 0.574088 0.035857
6
L’iterazione continua se l’errore relativo è ancora troppo grande
n = ...
ER = 0.01
eR = 1.00
xM = n/2
while(eR >= ER):
xA = xM
xB = n / xA
xM = (xA + xB) / 2
eA = abs(xA - xM)
eR = eA / xM
print("%8.4f %8.4f %8.4f %8.4f %8.4f"
%(xA, xB, xM, eA, eR))
128.0000 2.0000 65.0000 63.0000 0.9692
65.0000 3.9385 34.4692 30.5308 0.8857
34.4692 7.4269 20.9481 13.5212 0.6455
20.9481 12.2207 16.5844 4.3637 0.2631
16.5844 15.4362 16.0103 0.5741 0.0359
16.0103 15.9897 16.0000 0.0103 0.0006
import matplotlib.pyplot as plt
X =[]
XA=[]
XB=[]
XM=[]
n=256
ER=0.01
eR=1.00
xM=n/2
i=1
while(eR >= ER):
xA = xM
xB = n/xA
xM = (xA+xB)/2
eA = abs(xA-xM)
eR = eA/xM
print("%i %12.6f %12.6f %12.6f %12.6f %12.6f" %(i+1, xA, xB, xM, eA, eR))
X.append(i)
XA.append(xA)
XB.append(xB)
XM.append(xM)
i+=1
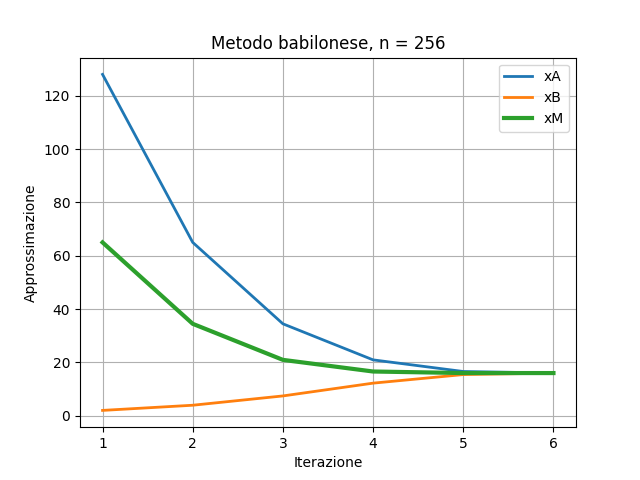
plt.grid()
plt.plot(X, XA, label="xA", linewidth="2")
plt.plot(X, XB, label="xB", linewidth="2")
plt.plot(X, XM, label="xM", linewidth="3")
plt.title("Metodo babilonese, n = " + str(n))
plt.xlabel("Iterazione")
plt.ylabel("Approsimazione")
plt.legend()
plt.show()
Forse è più chiaro con la soluzione approsssimata sull’asse delle ascisse?
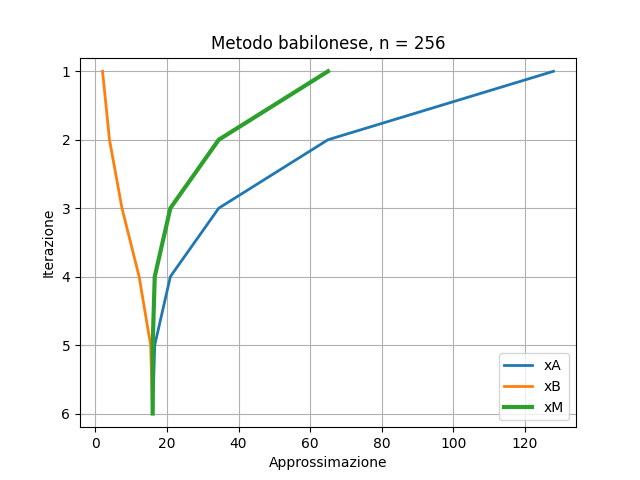
Nella funzione plt.plot() scrivi X dopo xA, xB, xM
import matplotlib.pyplot as plt
X =[]
XA=[]
XB=[]
XM=[]
n=256
ER=0.01
eR=1.00
xM=n/2
i=1
while(eR >= ER):
xA = xM
xB = n/xA
xM = (xA+xB)/2
eA = abs(xA-xM)
eR = eA/xM
print("%i %12.6f %12.6f %12.6f %12.6f %12.6f" %(i+1, xA, xB, xM, eA, eR))
X.append(i)
XA.append(xA)
XB.append(xB)
XM.append(xM)
i+=1
plt.grid()
plt.plot(XA, X, label="xA", linewidth="2")
plt.plot(XB, X, label="xB", linewidth="2")
plt.plot(XM, X, label="xM", linewidth="3")
plt.title("Metodo babilonese, n = " + str(n))
plt.xlabel("Approssimazione")
plt.ylabel("Iterazione")
plt.ylim(6.2, 0.8)
plt.legend()
plt.show()
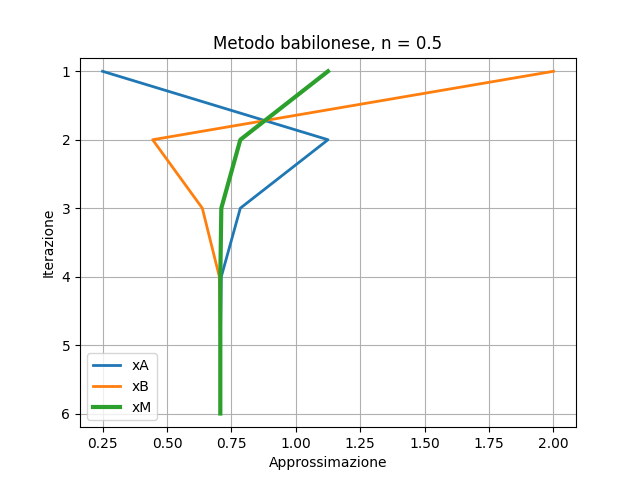
Se n < 4 al 2° passo ci sarà uno scambio tra xA e xB