Numeri di Fibonacci – Programmare con Python

Soluzione 1

Il primo esempio di programmazione nella home page di python.org visualizza la sequenza dei numeri di Fibonacci minori di 1000

def fib(n):
    a, b = 0, 1
    while a < n:
        print(a, end=' ')
        a, b = b, a+b
    print()

fib(1000)

Osserva l’output del codice (parte da 0…)

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987

Soluzione 2

Algoritmo iterativo: a partire dai valori noti (1, 1) si calcola un nuovo valore finché non si giunge all’indice richiesto

def fibonacci(n):
    if(n <= 2):
        return 1
    else:
        a = 1
        b = 1
        for i in range(n-2):
            c = a+b
            a = b
            b = c
        return c

fibonacci(10)

Visualizza Il 10° numero di Fibonacci, 55

Soluzione 3

Codice più corto

def fibonacci(n):
    a = 1
    b = 1
    for i in range(n-2):
        c = a+b
        a = b
        b = c
    return b

fibonacci(10)

Soluzione 4

Algoritmo ricorsivo: è molto sintetico

def fibonacci(n):
    if(n <= 2):
        return 1
    else:
        return fibonacci(n-1)+fibonacci(n-2)

Soluzione 5

Con formula: non è necessario alcun algoritmo iterativo o ricorsivo se si utilizza la formula

$\displaystyle f(n)=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$

import math

def fibonacci(n):
    r5 = math.sqrt(5)
    r  = 1/r5 * (math.pow((1+r5)/2, n) - math.pow((1-r5)/2, n))

    return round(r)

Soluzione 6

Il contributo del secondo termine è così piccolo che può essere trascurato: si ottiene il valore esatto calcolando il primo termine e arrotondando all’intero più vicino

$\displaystyle f(n) \approx \frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n$

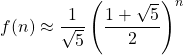
import math

def fibonacci(n):
    r5 = math.sqrt(5)
    r  = 1/r5 * math.pow((1+r5)/2, n)

    return round(r)