Numero di Eulero con limite

PASSI=100

for n in range(1,PASSI+1):
    en=(1+1/n)**n

    print("%3d | %.10f" %(n, en))

  1 | 2.0000000000
  2 | 2.2500000000
  3 | 2.3703703704
  4 | 2.4414062500
  5 | 2.4883200000
... | ...
100 | 2.7048138294

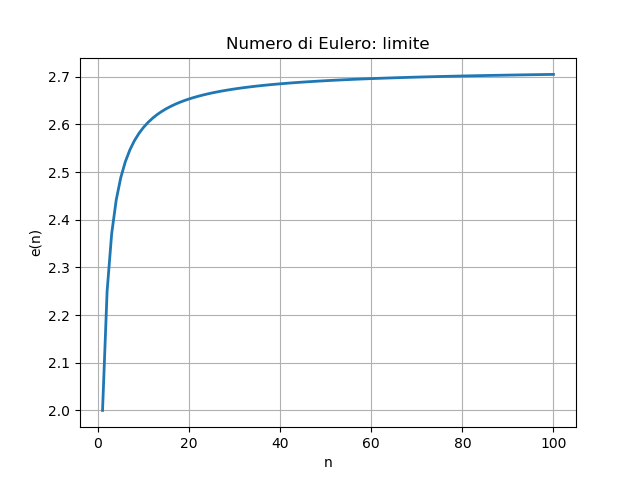
import matplotlib.pyplot as plt

PASSI=100

N=[]
E=[]

for n in range(1, PASSI+1):
    en=(1+1/n)**n

    print("%3d | %.10f" %(n, en))

    N.append(n)
    E.append(en)

plt.grid()
plt.plot(N,E, linewidth="2")
plt.title("Numero di Eulero: limite")
plt.xlabel("n")
plt.ylabel("e(n)")

plt.show()

import fractions

def f(n):
    x=fractions.Fraction(1, n)
    return (1+x)**n

PASSI=10
 
for n in range(1,PASSI+1):
    en=f(n)
 
    print("%2d | %23s | %.15f" %(n, en, en))

_1 |                       2 | 2.000000000000000
 2 |                     9/4 | 2.250000000000000
 3 |                   64/27 | 2.370370370370370
 4 |                 625/256 | 2.441406250000000
 5 |               7776/3125 | 2.488320000000000
 6 |            117649/46656 | 2.521626371742113
 7 |          2097152/823543 | 2.546499697040713
 8 |       43046721/16777216 | 2.565784513950348
 9 |    1000000000/387420489 | 2.581174791713197
10 | 25937424601/10000000000 | 2.593742460100000