Operazioni con vettori – 1

di

Considera tre vettori della stessa lunghezza

vettA = [2, 7, 1, 0, 1, 9, 9, 5]
vettB = [1, 2, 0, 4, 1, 9, 9, 7]
vettC = [1, 8, 0, 5, 1, 9, 9, 9]

Le operazioni seguenti producono un nuovo vettore.

Opposto / Prodotto per uno scalare

Scegli

  • appendi passo-passo gli elementi, moltiplicando per -1
  • utilizza il prodotto per uno scalare con k=-1

Somma

def somma(v1, v2): 
    n = len(v1)
    w = [] 
    for i in range(n): 
        x = v1[i]+v2[i]
        w.append(x) 
    return w 

def somma(v1, v2): 
    w = [] 
    for i in range(len(v1)): 
        w.append(v1[i]+v2[i]) 
    return w 

def somma(v1, v2): 
    w = [] 
    for x, y in zip(v1, v2): 
        w.append(x+y) 
    return w

Chiamate / Risultati

vettD = somma(vettA, vettB)  # [2,7,1,0,1,9,9,5] + [1,2,0,4,1,9,9,7] = [3, 9,1,4,2,18,18,12] 
vettE = somma(vettA, vettC)  # [2,7,1,0,1,9,9,5] + [1,8,0,5,1,9,9,9] = [3,15,1,5,2,18,18,14] 
vettF = somma(vettB, vettC)  # [1,2,0,4,1,9,9,7] + [1,8,0,5,1,9,9,9] = [2,10,0,9,2,18,18,16]

Differenza

Scegli

  • appendi passo-passo la sottrazione degli elementi, a_i-b_i
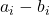
  • utilizza la somma con l’opposto del secondo vettore

Prodotto vettoriale

Da Wikipedia (dimensione 3…)

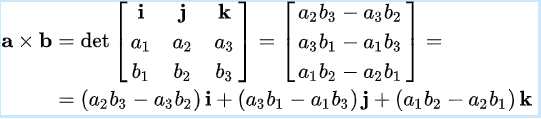
Gli indici in Python iniziano da zero…

def prodVett(a, b):
    c = 3*[0]
    c[0] = a[1]*b[2]-a[2]*b[1]
    c[1] = a[2]*b[0]-a[0]*b[2]
    c[2] = a[0]*b[1]-a[1]*b[0]
    return c

def prodVett(a, b):
    c = []
    c.append(a[1]*b[2]-a[2]*b[1])
    c.append(a[2]*b[0]-a[0]*b[2])
    c.append(a[0]*b[1]-a[1]*b[0])
    return c

vettA = [1, 0, 0]
vettB = [0, 1, 0]
vettC = [0, 0, 1]

vett1 = prodVett(vettA, vettA)  # [0, 0, 0]
vett2 = prodVett(vettA, vettB)  # [0, 0, 1]
vett3 = prodVett(vettA, vettC)  # [0,-1, 0]
vett4 = prodVett(vettB, vettA)  # [0, 0,-1]

I due vettori sono compatibili?

Alcune funzioni hanno senso solo se i due vettori sono compatibili (hanno la stessa lunghezza…)

Si potrebbe aggiungere un controllo preventivo

def funzione(v1, v2):
    n1 = len(v1)
    n2 = len(v2)
    if(n1 != n2): return None

    # Esegue il compito, se supera il controllo precedente
    # ...
    # ...