|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import math n=6 # Esagono # Raggio = 1 (Apotema circoscritto) Li = 1 # Poligono inscritto Ai = math.sqrt(1-(Li/2)**2) # Pi = n*Li # PIi = Pi/2 # Lc = Li/Ai # Poligono circoscritto Pc = n*Lc # PIc = Pc/2 # Delta = 1-Ai # Apotema circ. - apotema inscr. print("%5d - %18.16f %18.16f" %(n, PIi, PIc)) for passo in range(1,15): n=2*n Li = math.sqrt((Li/2)**2+Delta**2) Ai = math.sqrt(1-(Li/2)**2) Pi = n*Li PIi = Pi/2 Lc = Li/Ai Pc = n*Lc PIc = Pc/2 Delta=1-Ai print("%5d - %18.16f %18.16f" %(n, PIi, PIc)) |
Si ottiene
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
6 - 3.0000000000000000 3.4641016151377553 12 - 3.1058285412302489 3.2153903091734723 24 - 3.1326286132812378 3.1596599420975000 48 - 3.1393502030468667 3.1460862151314348 96 - 3.1410319508905098 3.1427145996453683 192 - 3.1414524722854624 3.1418730499798242 384 - 3.1415576079118579 3.1416627470568486 768 - 3.1415838921483186 3.1416101766046900 1536 - 3.1415904632280505 3.1415970343215260 3072 - 3.1415921059992717 3.1415937487713523 6144 - 3.1415925166921577 3.1415929273850973 12288 - 3.1415926193653840 3.1415927220386139 24576 - 3.1415926450336911 3.1415926707019981 49152 - 3.1415926514507682 3.1415926578678448 98304 - 3.1415926530550373 3.1415926546593065 |
matplotlib
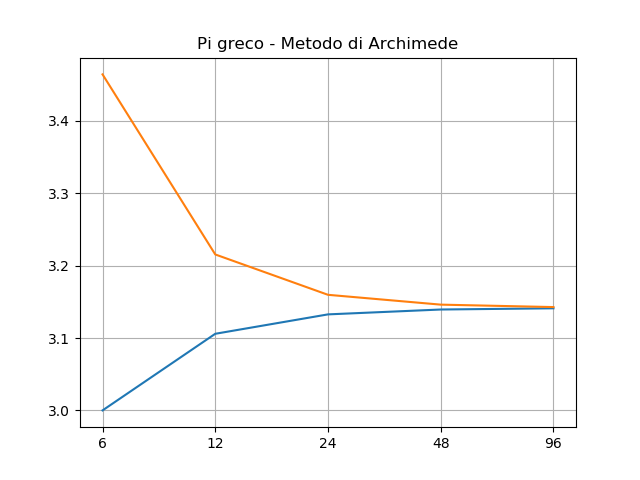
Per numero di lati fino a 96
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
import math import matplotlib.pyplot as plt N = [6*2**i for i in range(0,5)] PII = 5*[0] PIC = 5*[0] n = N[0] Li = 1 # Poligono inscritto Ai = math.sqrt(1-(Li/2)**2) # Pi = n*Li # PIi = Pi/2 # Lc = Li/Ai # Poligono circoscritto Pc = n*Lc # PIc = Pc/2 # Delta = 1-Ai # Apotema circ. - apotema inscr. PII[0]=PIi PIC[0]=PIc print("%5d - %18.16f %18.16f" %(n,PIi, PIc)) for passo in range(1,5): n=N[passo] Li = math.sqrt((Li/2)**2+Delta**2) Ai = math.sqrt(1-(Li/2)**2) Pi = n*Li PIi = Pi/2 Lc = Li/Ai Pc = n*Lc PIc = Pc/2 Delta = 1-Ai PII[passo]=PIi PIC[passo]=PIc print("%5d - %18.16f %18.16f" %(n,PIi, PIc)) plt.grid(which="major") plt.plot(PII) plt.plot(PIC) plt.title("Pi greco - Metodo di Archimede") plt.xticks(range(0,5), N) plt.show() |