import math
QUANTE = 10 # SCEGLI UN VALORE A PIACERE
r = ___ # SCEGLI UN VALORE A PIACERE
n = 6 # Il primo poligono è un esagono
l = r # Il lato del 1° poligono (esagono) è uguale al raggio della circonferenza
p = n*l # n*lato
pi = p/(2*r) # Perimetro/Diametro
a = math.sqrt(r*r-(l/2)**2) # "Ipotenusa..."
d = r-a # ...
print(pi) # 1° approssimazione
for passo in range(1,QUANTE):
n = 2*n # Il numero di lati raddoppia
l = math.sqrt((l/2)**2+d**2) # "Ipotenusa..."
p = n*l # ...
pi = p/(2*r) # ...
a = math.sqrt(r*r-(l/2)**2) # ...
d = r-a #
print(pi) # Approssimazioni successive
Si ottiene la sequenza
3.0
3.105828541230249
3.1326286132812378
3.1393502030468667
3.14103195089051
3.1414524722854624
3.141557607911858
3.1415838921483186
3.1415904632280505
3.1415921059992717
Il modulo permette di calcolare il risultato
- in modo simbolico (precisione infinita)
- nella codifica LaTeX (per la stampa)
- con precisione a piacere
import math
import sympy as sp # Modulo SymPy
QUANTE = 5
sp.init_printing() # Abilita pprint()
r = sp.symbols('r') # Raggio della circonferenza
n = sp.symbols('n') # Numero di lati del poligono
l = sp.symbols('l') # Lato del poligono
p = sp.symbols('p') # Perimetro del poligono
pi = sp.symbols('pi') # Approssimazione di pi greco
a = sp.symbols('a') # Apotema del poligono
d = sp.symbols('d') # Differenza tra il raggio e l'apotema
n = 6 # Il primo poligono è un esagono
l = r # Il lato è uguale al raggio della circonferenza
p = n*l # n*lato
pi = p/(2*r) # Perimetro/Diametro
a = sp.sqrt(r*r-(l/2)**2) # "Ipotenusa..."
d = r-a # ...
PIGRECO = sp.simplify(pi.subs(r, 1)) # Sostituisce e semplifica
sp.pprint(PIGRECO) # Stampa la formula in forma comprensibile
print(sp.latex(PIGRECO)) # in LaTeX
print(PIGRECO.evalf(20)) # 20 cifre dopo la virgola
for passo in range(1,QUANTE):
n = 2*n # Il numero di lati raddoppia
l = sp.sqrt((l/2)**2+d**2) # "Ipotenusa..."
p = n*l # ...
pi = p/(2*r) # ...
a = sp.sqrt(r*r-(l/2)**2) # ...
d = r-a # ...
PIGRECO = sp.simplify(pi.subs(r, 1))
sp.pprint(PIGRECO)
print(sp.latex(PIGRECO))
print(PIGRECO.evalf(20))
Osserva
- import sympy as sp
- sp.init_printing() Abilita la stampa amichevole
- sp.symbols(…) Definisce una variabile formale
- sp.sqrt(…) Calcola, formalmente, la radice quadrata
- pi.subs(r, 1) Sostituisce il valore della variabile
- sp.simplify(…) Semplifica la formula
- sp.pprint(…) Stampa in forma amichevole
- sp.latex(…) Converte in formato LaTeX
- ___.evalf(20) Calcola 20 cifre dopo la virgola
Si ottiene
3
3
3.0000000000000000000
________
6⋅╲╱ 2 - √3
6 \sqrt{2 - \sqrt{3}}
3.1058285412302491482
________________
╱ ________
12⋅╲╱ 2 - ╲╱ √3 + 2
12 \sqrt{2 - \sqrt{\sqrt{3} + 2}}
3.1326286132812381972
_________________________
╱ ________________
╱ ╱ ________
24⋅╲╱ 2 - ╲╱ ╲╱ √3 + 2 + 2
24 \sqrt{2 - \sqrt{\sqrt{\sqrt{3} + 2} + 2}}
3.1393502030468672071
___________________________________
╱ _________________________
╱ ╱ ________________
╱ ╱ ╱ ________
48⋅╲╱ 2 - ╲╱ ╲╱ ╲╱ √3 + 2 + 2 + 2
48 \sqrt{2 - \sqrt{\sqrt{\sqrt{\sqrt{3} + 2} + 2} + 2}}
3.1410319508905096381
Ecco le approssimazioni successive in formato LaTeX (con qualche commutazione)
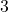
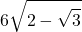
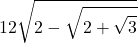
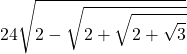
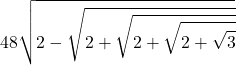
- …