Esame di Stato 2003 – 5

di

La funzione 2x^3 - 3 x^2 + 2 ha un solo zero reale, vale a dire che il suo grafico interseca una sola volta l’asse delle ascisse.
Fornire un’esauriente dimostrazione di questo fatto e stabilire se lo zero della funzione è positivo o negativo.

Esistenza

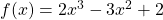  • f(x) = 2x^3 - 3 x^2 + 2, continua in R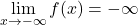
  • \displaystyle \lim_{x\to-\infty}f(x)=-\infty
  • \displaystyle \lim_{x\to +\infty}f(x)=+\infty
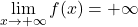
  • Teorema degli zeri: esiste almeno uno zero in R.
    Tutte le funzioni polinomiali di grado dispari hanno almeno uno zero reale.

Unicità

  • f'(x) = 6x^2-6x = 6x(x-1)
  • f'(x) = 0
    • x_1 = 0
    • x_2 = 1
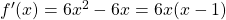
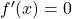
  • x < 0: f'(x) > 0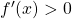, f(x) crescente
  • 0 < x < 1: 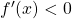f'(x) < 0, f(x) decrescente
  • x > 1: 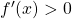f'(x) > 0, f(x) crescente
  • x=0, 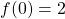f(0)=2, massimo relativo
  • x=1, 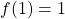f(1)=1, minimo relativo
  • x > 0: f(x) > 0
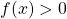
  • x < 0: f(x) crescente, un solo zero reale

Valore

  • f(-1) = -3
  • f(0) = 2
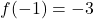
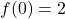
  • La funzione ha segni discordi in [-1, 0]
  • Teorema degli zeri: esiste x0 in (-1, 0) tale che f(x0) = 0

Conclusione

La funzione ha un solo zero reale ed è negativo.

Approssimazione

…