Esame di Stato 2007 PNI – 6

di

Si scelga a caso un punto P all’interno di un triangolo equilatero il cui lato ha una lunghezza 3.
Si determini la probabilità che la distanza di P da ogni vertice sia maggiore di 1.

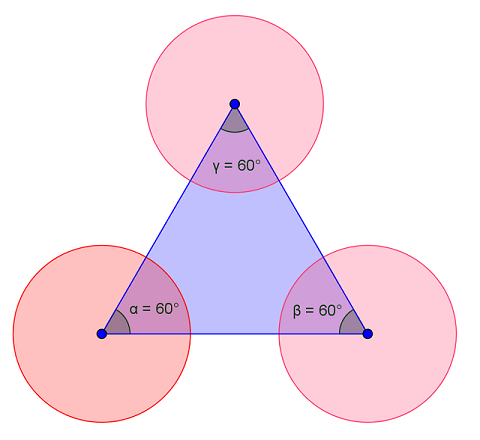
Osserva la figura a destra

Il triangolo

  • è equilatero
  • lato = 3 cm
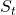  • S_t superficie?

Ciascun cerchio

  • raggio = 1 cm
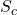  • S_c superficie?

I 3 settori circolari

  • raggio = 1 cm
  • α = β = γ = 60°
  • α+β+γ = 180°
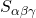  • S_{\alpha\beta\gamma} superficie?

Calcoli

  1. \displaystyle S_t = \dots = \frac{9}{4}\sqrt{3} cm²
  2. \displaystyle S_c = \dots = \pi cm²
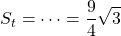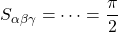  3. \displaystyle S_{\alpha\beta\gamma} = \dots = \frac{\pi}{2} cm²

La probabilità che il punto P cada a una distanza maggiore di 1 da ogni vertice è data dal rapporto tra …

\displaystyle p=\frac{S_t - S_{\alpha\beta\gamma}}{S_t}=1 - \frac{S_{\alpha\beta\gamma}}{S_t} = … = 0,5969…

quindi la probabilità è circa del 60%