Esame di Stato 2003 PNI – 6

2024-05-052017-02-11 di admin

Si vuole che l’equazione $x^3+bx-7$ abbia 3 radici reali.
Qual è un possibile valore di b?

Sia $f(x) = x^3+bx-7$

Osserva

$\displaystyle \lim_{x\to-\infty}f(x)=-\infty$
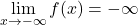
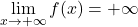$\displaystyle \lim_{x\to+\infty}f(x)=+\infty$ , almeno uno zero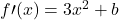
$f\prime(x)=3x^2+b$
- $3x^2+b=0$
- $\displaystyle x=\pm \sqrt{\frac{-b}{3}},\ b\ \le \ 0$

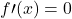
Per b=-3

$f(x)=x^3-3x-7$
$f\prime(x)=3x^2-3$
- $3x^2-3=0$
- $x=\pm1$
$f(-1) = -1+3-7 = -5$
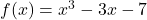
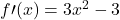
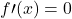
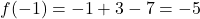
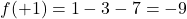$f(+1) = 1-3-7 = -9$ , i punti notevoli sono concordi… un solo zero.

Per b=-12

$f(x)=x^3-12x-7$
$f\prime(x)=3x^2-12$
- $3x^2-12=0$
- $x=\pm2$
$f(-2)=-8+24-7=+9$
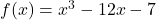
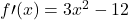
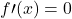
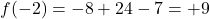
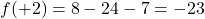$f(+2)=8-24-7=-23$ , i punti notevoli sono discordi… tre zeri.