Esame di Stato 2004 PNI – 9

Si dimostri che l’equazione $e^x +3 x = 0$ ammette una e una solo soluzione e se ne calcoli un valore approssimato utilizzando un metodo iterativo a scelta.

Esame di Stato 2004 – 4

Dimostrate che l’equazione $e^x +3 x = 0$ ammette una e una sola soluzione reale.

Sia

$f(x) = e^x +3 x$

Esistenza

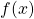$f(x)$ continua in R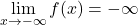
$\displaystyle\lim_{x \rightarrow -\infty} f(x) = -\infty$
$\displaystyle\lim_{x \rightarrow +\infty} f(x) = +\infty$
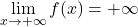
Esiste M in R tale che f(-M) < 0, f(M) > 0.
Teorema degli zeri: esiste almeno uno zero in R.

Unicità

$f'(x) = e^x + 3$
$f'(x) > 0$
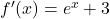
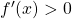
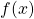$f(x)$ crescente in R
Lo zero è unico

Approssimazione

$f(0) = 1 > 0$
$\displaystyle f(-1) = \frac{1}{e}-3 > 0$
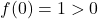
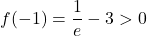
Uno zero in [-1, 0]

L’equazione ammetta una e una sola soluzione reale x₀ in [-1, 0]

Se ne calcoli un valore approssimato utilizzando un metodo iterativo a scelta.