Si determini la probabilità che, lanciando 8 volte una moneta non truccata, si ottenga 4 volte testa.
Soluzione 1
Calcola le probabilità
- TESTA con un lancio:

- CROCE con un lancio:

- 4 volte TESTA con 8 lanci:
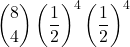 =
= 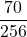 = 0,2734… = 27,34…%
= 0,2734… = 27,34…%
Soluzione 2
Il numero di parole (anagrammi) con 2 lettere diverse
- con 4 TESTA e 4 CROCE:
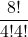 = 70
= 70 - di lunghezza 8:
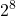 = 256
= 256
Considera il rapporto
p = ![]() = …
= …
Esercizio
Calcola tutte le probabilità di fare TESTA con 8 lanci di una moneta…
- 0 volte:
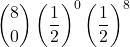 =
= 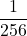 = 0,003906…
= 0,003906… - 1 volta:
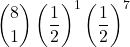 =
= 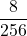 = 0,03125
= 0,03125 - 2 volte:
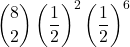 =
= 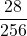 = 0,109375
= 0,109375 - 3 volte:
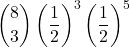 =
= 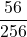 = 0,21875
= 0,21875 - 4 volte:
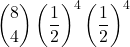 =
= 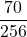 = 0,273437…
= 0,273437… - 5 volte:
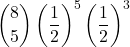 =
= 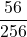 = 0,21875
= 0,21875 - 6 volte:
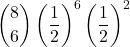 =
= 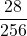 = 0,109375
= 0,109375 - 7 volte:
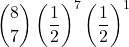 =
= 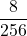 = 0,03125
= 0,03125 - 8 volte:
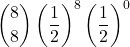 =
= 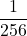 = 0,003906…
= 0,003906…